北京市海淀区初三第一学期期末数学卷
已知一个直角三角形纸片 ,其中
,其中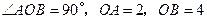 .如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边
.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边 交于点
交于点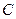 ,与边
,与边 交于点
交于点 .
.
(1)若折叠后使点 与点
与点 重合,求点
重合,求点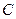 的坐标;
的坐标;
(2)若折叠后点 落在边
落在边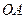 上的点为
上的点为 ,设
,设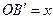 ,
,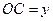 ,试写出
,试写出 关于
关于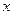 的函数解析式,并确定
的函数解析式,并确定 的取值范围;
的取值范围;
(3)若折叠后点 落在边
落在边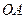 上的点为
上的点为 ,且使
,且使 ,求此时点
,求此时点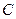 的坐标.
的坐标.
如图,已知抛物线与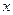 轴交于点
轴交于点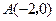 ,
,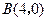 ,与
,与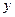 轴交于点
轴交于点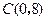 .
.
(1)求抛物线的解析式及其顶点 的坐标;
的坐标;
(2)设直线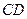 交
交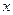 轴于点
轴于点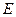 .在线段
.在线段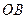 的垂直平分线上是否存在点
的垂直平分线上是否存在点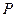 ,使得点
,使得点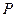 到直线
到直线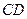 的距离等于点
的距离等于点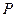 到原点
到原点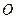 的距离?如果存在,求出点
的距离?如果存在,求出点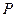 的坐标;如果不存在,请说明理由;
的坐标;如果不存在,请说明理由;
(3)过点 作
作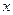 轴的垂线,交直线
轴的垂线,交直线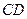 于点
于点 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段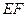 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
若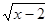 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
| A. x≥-2 | B. x≠-2 | C. x≥2 | D. x≠2 |
下列各点,不在函数y="2x" -1的图象上的是( )
| A.(2,3) | B.(-9,-5) | C.(O,-1) | D.(-1,0) |
下列各式:①XL一xy’;②X2一xy+2y2;③_X2+ y2;④X2—2xy+y2,其中能用
公式法分解因式的有
| A.1个 | B.2个 | C.3个 | D.4个 |
下列计算:
①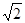 +
+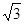 =
=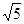 ;②2a
;②2a ·3a
·3a = 6a
= 6a ;③(2x+y)(x-3y)=2x
;③(2x+y)(x-3y)=2x -5xy -3y
-5xy -3y ;
;
④(x+ y) =x
=x + y
+ y .其中计算错误的个数是( )
.其中计算错误的个数是( )
| A.O个 | B.l个 | C.2个 | D.3个 |
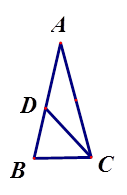
如图,点A在线段BC的垂直平分线上,AD=DC,∠ A=28°,则∠BCD的度数为( )
| A.76° | B.62° | C.48° | D.38° |
如果直线y=ax+2与直线y="bx" -3相交于x轴上的同一点,则a:b等于 ( )
A.-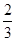 |
B.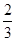 |
C.- |
D. |
甲、乙两人以相同路线前往距离工作单位10km的培训中心参加学习.图中l甲、,l乙分别表示甲、乙两人前往目的地所走的路程S (km)随时间t变化的函数图象,以下说法:①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;⑧乙走了8km后遇到甲;④乙出发6分钟后追上甲,其中正确的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
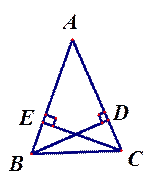
如图:△ABC中,∠ACB=90°,∠CAD=30°,AC="BC=AD," CE⊥CD,且CE=CD,连接BD. DE. BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥ BE;④ =1.其中正确的
=1.其中正确的
A.①②③ B.①②④ C.①⑧④ D.①②⑧④
如图,点D、E在△ABC的BC边上,.∠ BAD=∠CAE,要推理得出△ABF≌△ACD,可以补充的一个条件是__________________.(不添加辅助线,写出一个即可)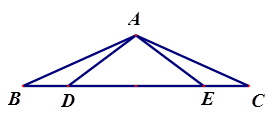
如图,直线l1 y1:= kx+b与直线l2:y2=mx+n交点为P(1,1),当y1>y2>0时,x的取值范围是________


(1)点(1,3)沿X轴的正方向平移4个单位得到的点的坐标是_________
(2)直线y=3x沿x轴的正方向平移4个单位得到的直线解析式为____________
(3)若直线l与(2)中所得的直线关于直线x=2对称,试求直线l的解析式.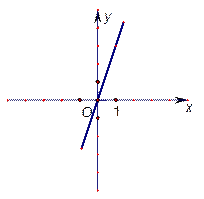
玉树地震发生后,根据救灾指挥中心的信息,甲、乙两个重灾区急需一种大型挖掘机,甲地需要27台,乙地需要25台;A、B两省获知情况后慷慨相助,分别捐赠该型号挖掘机28台和24台,并将其全部调运往灾区,如果从A省调运一台挖掘机到甲地耗资0.4万元,到乙地耗资0.3万元;从B省调运一台挖掘机到甲地耗资0.5万元,到乙地耗资0.2万元;设从A调往甲地x台挖掘机,A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元: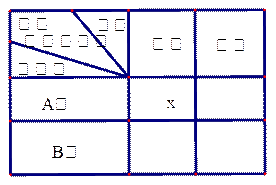
(1)请完成表格的填空:
(2)求出y与x之间的函数关系式,并直接写出自变量x的取值范围
(3)画出这个函数的图象,结合图象说明若要使总耗资不超过16.2万元,有哪几种调运方案?哪种调运方案的总耗资最少?
已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( )
| A.外离 | B.外切 | C.相交 | D.内切 |
如图,⊙O是△ABC的外接圆,已知∠ABO=30º,则∠ACB的大小为 ( )
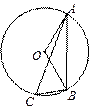

| A.60º | B.30º | C.45º | D.50º |
如图,有一枚圆形硬币,如果要在这枚硬币的周围摆放几枚与它完全相同的硬币,使得周围的硬币都和这枚硬币相外切,且相邻的硬币相外切,则这枚硬币周围最多可摆放
| A.4枚硬币 | B.5枚硬币 | C.6枚硬币 | D.8枚硬币 |
圆锥的母线长是3,底面半径是1,则这个圆锥侧面展开图圆心角的度数为
| A.90° | B.120° | C.150° | D.180° |
如图,E,B,A,F四点共线,点D是正三角形ABC的边AC的中点,点 是直线
是直线 上异于A,B的一个动点,且满足
上异于A,B的一个动点,且满足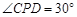 ,则 ( )
,则 ( )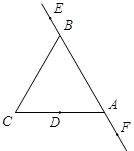
A.点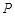 一定在射线 一定在射线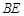 上 上 |
B.点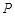 一定在线段 一定在线段 上 上 |
C.点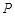 可以在射线 可以在射线 上,也可以在线段 上,也可以在线段 上 上 |
D.点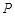 可以在射线 可以在射线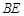 上,也可以在线段 上,也可以在线段 上 上 |
如图,圆形转盘中,A,B,C三个扇形区域的圆心角分别为150°,120°和90°. 转动圆盘后,指针停止在任何位置的可能性都相同(若指针停在分界线上,则重新转动圆盘),则转动圆盘一次,指针停在B区域的概率是 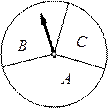
(1) 如图一,等边三角形MNP的边长为1,线段AB的长为4,点M与A重合,点N在线段AB上. △MNP沿线段AB按 的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;
的方向滚动, 直至△MNP中有一个点与点B重合为止,则点P经过的路程为 ;
(2)如图二,正方形MNPQ的边长为1,正方形ABCD的边长为2,点M与点A重合,点N在线段AB上, 点P在正方形内部,正方形MNPQ沿正方形ABCD的边按 的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为 .
的方向滚动,始终保持M,N,P,Q四点在正方形内部或边界上,直至正方形MNPQ回到初始位置为止,则点P经过的最短路程为 .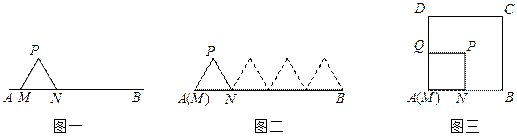
(注:以△MNP为例,△MNP沿线段AB按 的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时, 再以顶点P为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)
的方向滚动指的是先以顶点N为中心顺时针旋转,当顶点P落在线段AB上时, 再以顶点P为中心顺时针旋转,如此继续. 多边形沿直线滚动与此类似.)
某射击运动员在相同条件下的射击160次,其成绩记录如下:
| 射击次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
| 射中9环以上的次数 |
15 |
33 |
|
63 |
78 |
97 |
111 |
127 |
| 射中9环以上的频率 |
0.75 |
0.83 |
0.80 |
0.79 |
0.79 |
|
0.79 |
0.81 |
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),并简述理由.
如图,正方形 中,点F在边BC上,E在边BA的延长线上,
中,点F在边BC上,E在边BA的延长线上,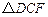 按顺时针方向旋转后能与
按顺时针方向旋转后能与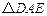 重合.
重合.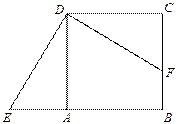
(1)旋转中心是点 ;最少旋转了 度;
(2)若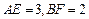 ,求四边形
,求四边形 的面积.
的面积.
随着人们节能意识的增强,节能产品的销售量逐年增加.某地区高效节能灯的年销售量2009年为10万只,预计2011年将达到14.4万只.求该地区2009年到2011年高效节能灯年销售量的平均增长率
如图,在△ABC中,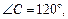
 ,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E.
,半圆的圆心O在AB上,且与AC,BC分别相切于点D,E.
(1)求半圆O的半径;
(2)求图中阴影部分的面积.
如图,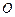 为正方形
为正方形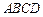 对角线AC上一点,以
对角线AC上一点,以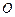 为圆心,
为圆心,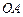 长为半径的⊙
长为半径的⊙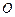 与
与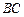 相切于点
相切于点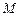 .
.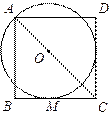
(1)求证: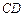 与⊙
与⊙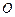 相切;
相切;
(2)若⊙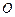 的半径为1,求正方形
的半径为1,求正方形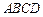 的边长.
的边长.
一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程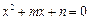 有两个不相等实数根的概率.
有两个不相等实数根的概率.
如图一,AB是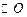 的直径,AC是弦,直线EF和
的直径,AC是弦,直线EF和 相切与点C,
相切与点C,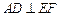 ,垂足为D.
,垂足为D.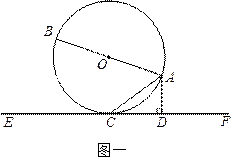
(1)求证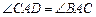 ;
;
(2)如图二,若把直线EF向上移动,使得EF与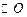 相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与
相交于G,C两点(点C在点G的右侧),连结AC,AG,若题中其他条件不变,这时图中是否存在与 相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.
(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是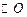 的切线,连接OQ. 求
的切线,连接OQ. 求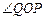 的大小;
的大小;
(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被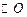 截得的弦长
截得的弦长

 x
x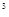 =
=
 )
)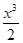

 最接近的整数是( )
最接近的整数是( )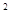 -b
-b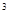 ="_____," 24x
="_____," 24x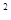 y-(-6xy)="_______," ,
y-(-6xy)="_______," , =___
=___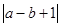 与
与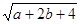 互为相反数,则
互为相反数,则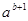 =______
=______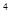 y
y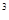 -35x
-35x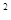 +7x
+7x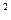 y- 6xy
y- 6xy
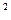 +y
+y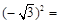 ( )
( )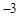
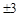
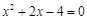
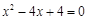

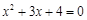
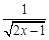 有意义,则x的取值范围是
有意义,则x的取值范围是 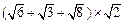
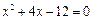
 中,AB是
中,AB是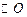 的直径,
的直径,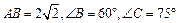 ,求
,求 的度数
的度数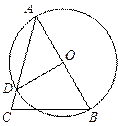
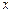 的方程
的方程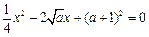 有实根.
有实根. 的值;
的值; 的所有根均为整数,求整数
的所有根均为整数,求整数 的值
的值 和半圆
和半圆 ,其中
,其中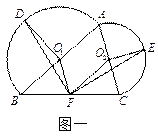
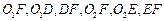 ,证明:
,证明: ;
;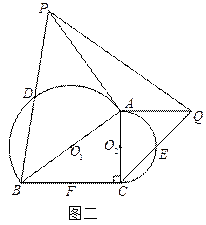
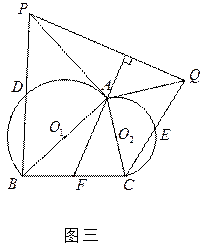
 粤公网安备 44130202000953号
粤公网安备 44130202000953号