初中数学二次函数在给定区间上的最值试题

某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）当销售单价为70元时，每天的销售利润是多少？
（2）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式，并求出自变量的取值范围；
（3）如果该企业每天的总成本不超过7000元，那么销售单价为多少元时，每天的销售利润最大？最大利润是多少？（每天的总成本＝每件的成本×每天的销售量）

如图，已知二次函数的图象经过A（2，0）、B（0，－6）两点．
（1）求这个二次函数的解析式
（2）设该二次函数的对称轴与轴交于点C，连接BA、BC，求∆ABC的面积．

一个足球从地面上被踢出，它距地面高度y（米）可以用二次函数y=－4．9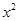+19．6x刻画，其中x（秒）表示足球被踢出后经过的时间．则足球被踢出后到离开地面达到最高点所用的时间是        秒．

已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列4个结论：
①abc＜0；②b＞a+c；③2a-b=0；④b²-4ac＜0．其中正确的结论个数是（   ）

A．1个

B．2个

C．3个

D．4个

如图一条抛物线（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．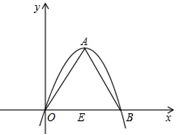

（1）“抛物线三角形”一定是_______________三角形；
（2）若抛物线y=－x²+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；
（3）如图，△OAB是抛物线y=－x²+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由．

已知二次函数的图象与y轴相交于点（0，3），并经过点（-2，5），它的对称轴是x=1，求这个函数的解析式，并写出这个函数图象的顶点坐标．

二次函数的图象交x轴于A、B两点，交y轴于点C，则△ABC的面积为        ．

某商场将每件进价为160元的某种商品原来按每件200元出售，一天可售出100件，后来经过市场调查，发现这种商品单价每降低2元，其销量可增加10件．
（1）求商场经营该商品原来一天可获利润多少元？
（2）设后来该商品每件降价x元，商场一天可获利润y元．
①若商场经营该商品一天要获利润4320元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，当x取何值时，商场获利润最大？并求最大利润值．

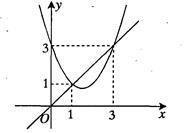
已知二次函数y＝ax²＋bx＋c与一次函数y＝x的图象如图所示，给出以上结论：
①b²－4ac>0；
②a＋b＋c＝1；
③当1<x<3时，ax²＋（b－1）x＋c<0；
④二次函数y＝ax²＋（b－1）x＋c的图象经过点（1，0）和（3，0）．
其中正确的有：        （把你认为正确结论的序号都填上）．

直线y=ax－6与抛物线y=+4x+3只有一个交点，则a的值为          ．

抛物线y=（k+1）x²+k²-9开口向下，且经过原点，则k＝      ．

已知两点（－2，y₁）（3，y₂）均在抛物线y＝ax²＋bx＋c上，点C（x₀，y₀）是该抛物线的顶点，若y₁<y₂≤y₀，则x₀的取值范围是（    ）

A．x0>3

B．x0>

C．－2<x0<3

D．－1<x0<

已知二次函数y＝ax²＋bx＋c，若a<0，c>0，那么它的图象大致是（    ）

设函数（k是常数）．
（1）当k=1和k=2时的函数和的图像如图所示，请你在同一坐标系中画出k=3时函数的图像；

（2）根据图像，写出你发现的两条结论；
（3）将函数的图像向左平移2个单位，再向下平移4个单位，得到函数的图像。请写出函数的解析式，回答自变量x取何值时，函数的最小值是多少？

二次函数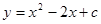的图象与x轴的一个交点坐标为（3，0），则与y轴的交点坐标为           ．