初中数学二次函数在给定区间上的最值试题

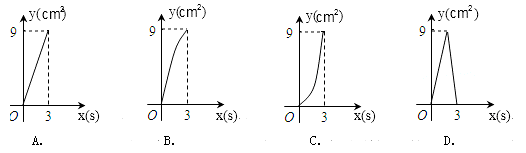
如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=6cm，动点P从点C沿CA，以1cm/s的速度向点A运动，同时动点O从点C沿CB，以2cm/s的速度向点B运动，其中一个动点到达终点时，另一个动点也停止运动．则运动过程中所构成的△CPO的面积y（cm²）与运动时间x（s）之间的函数图象大致是（ ）

已知二次函数y=﹣x²+2x+3，当x≥2时，y的取值范围是（ ）

A．y≥3

B．y≤3

C．y≥4

D．y≤4

一次函数y=kx-3的图象经过点（1，-2）．
（1）求这个一次函数关系式；
（2）点（2，-1）是否在此函数的图象上？说明理由；
（3）当x为何值时，y≤0？

已知抛物线y=ax²＋bx＋c的部分图象如图所示，若y＞0，则x的取值范围是________．

抛物线y =2x²+8x+m与x轴只有一个公共点，则m值为       ．

函数y=a（x-1）²，y=ax+a的图象在同一坐标系的图象可能是（  ）

为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌
粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．
（1）试求出每天的销售量y（盒）与每盒售价 （元）之间的函数关系式；
（2）当每盒售价定为多少元时，每天销售的利润 （元）最大？最大利润是多少？

请在同一坐标系中画出二次函数①；②的图象。说出两条抛物线的位置关系，指出②的开口方向、对称轴和顶点坐标及增减性。

已知点都在二次函数的图象上，则
的大小关系是            ．

如图，二次函数的图象与轴交于，两点，与轴交 于点，且．则下列结论：①②；③；④．其中正确结论的个数是（   ）

A．4

B．3

C．2

D．1

如图，对称轴为直线x=﹣1的抛物线y=ax²+bx+c（a≠0）与x轴相交于A、B两点，其中点A的坐标为（﹣3，0）．

（1）求点B的坐标；
（2）已知a=1，C为抛物线与y轴的交点．
①若点P在抛物线上，且S_△POC=4S_△BOC．求点P的坐标；
②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．

某体育休闲超市购进一种成本为20元/个的风筝，据市场调查分析，若按25元/个销售，一个月能售出70个，在此基础上，售价每涨1元/个，月销售量就减少2个．设这种风筝的销售单价为x（元/个），该超市每月销售这种风筝的所获得的利润为y（元），针对这种风筝的销售情况，请解答下列问题:
（1）用含x的代数式分别表示出每个风筝的销售利润为           元，每月卖出的风筝的个数是            个；
（2）求y与x之间的函数关系式；
（3）若该超市想在每月销售这种风筝的成本不超过800元的情况下，使得月销售利润达到600元，则每个风筝的售价应定为多少元?

如图，已知抛物线y=x²+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是  ．

如图，二次函数y=ax²+bx+c的图象经过点（0，﹣2），与x轴交点的横坐标分别为x₁，x₂，且﹣1＜x₁＜0，1＜x₂＜2，下列结论正确的是（ ）

A．a＜0	B．a﹣b+c＜0
C．	D．4ac﹣b^2＜﹣8a

如图，在直角坐标系中，已知P（-2，-1），点T（t，0）是x轴上的一个动点．

（1）求点P关于原点的对称点M的坐标．
（2）已知点N（0，2）为y轴上的一点，求经过P、M、N三点的抛物线的解析式，并求出该抛物线的顶点坐标．
（3）点T在运动过程中，是否存在某个时刻使△MTO为等腰三角形？若存在，求出点T的坐标．若不存在，请说明理由．