初中数学二次函数在给定区间上的最值试题

如图是二次函数y=ax²+bx+c的部分图象，由图象可知该二次函数的对称轴是（   ）

A．直线x=－1

B．直线x=2

C．直线x=5

D．直线x=0

将抛物线向左平移2个单位后，得到的抛物线的解析式是（ ）

A．	B．
C．	D．

如图，在平面直角坐标系中，顶点为（4，﹣1）的抛物线交y轴于A点，交x轴于B，C两点（点B在点C的左侧），已知A点坐标为（0，3）．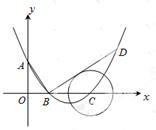

（1）求此抛物线的解析式
（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C有怎样的位置关系，并给出证明；
（3）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积．

如图，抛物线与轴交于，两点，与轴交于点，且．

（1）求抛物线的解析式及顶点的坐标；
（2）判断的形状，证明你的结论；
（3）点是轴上的一个动点，当的值最小时，求的值．

某校九年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作．已知该水果的进价为8元/千克，下面是他们在活动结束后的对话．
小丽：如果以10元/千克的价格销售，那么每天可售出300千克．
小强：如果每千克的利润为3元，那么每天可售出250千克．
小红：如果以13元/千克的价格销售，那么每天可获取利润750元．
【利润=（销售价-进价）销售量】
（1）请根据他们的对话填写下表：

销售单价x（元/kg）	10	11	13
销售量y（kg）

（2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系．并求y（千克）与x（元）（x＞0）的函数关系式；
（3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式．当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？

如图，抛物线y＝－x²＋bx＋c与x轴交于A、B两点，与y轴交于点C，点O为坐标原点，点D为抛物线的顶点，点E在抛物线上，点F在x轴上，四边形OCEF为矩形，且OF＝2，EF＝3，

（1）求抛物线所对应的函数解析式；
（2）求△ABD的面积；

如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线与扇形OAB的边界总有两个公共点，则实数k的取值范围是____________．

已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表：

x	…	﹣1	0	1	2	3	…
y	…	10	5	2	1	2	…

 
则当y＜5时，x的取值范围是        ．

将抛物线沿轴向左平移个单位长度所得抛物线的关系式为      ．

将一条抛物线向左平移2个单位后得到了y=2x²的函数图象，则这条抛物线是（  ）  

A．y=2x^2+2	B．y=2x^2－2
C．y=2（x－2）^2	D．y=2（x+2）^2

二次函数（为常数且）中的与的部分对应值如下表：

 
给出了结论：
（1）二次函数有最小值，最小值为；
（2）若，则的取值范围为； 
（3）二次函数的图象与轴有两个交点，且它们分别在轴两侧．
则其中正确结论的个数是 （   ）
       B．           C．         D． 

如图：抛物线y=－+bx+c与x轴交于A、B两点，与y轴交于点C，且∠BAC=α，∠ABC=，tanα－tanβ=2，∠ACB=90°．

（1）求点C的坐标；
（2）求抛物线的解析式；
（3）若抛物线的顶点为P，求四边形ABPC的面积．

如图，抛物线经过A（，0），B（，0），C（0，2）三点．

（1）求抛物线的解析式；
（2）在直线AC下方的抛物线上有一点D，使得△DCA的面积最大，求点D的坐标；
（3）设点M是抛物线的顶点，试判断抛物线上是否存在点H满足？若存在，请求出点H的坐标；若不存在，请说明理由．

函数与（）在同一直角坐标系中的图象可能是（ ）

A．

B．

C．

D．

如图，圆心在坐标原点的⊙O的半径为1，若抛物线和⊙O刚好有三个公共点，则此时______ ，若抛物线和⊙O只有两个公共点，则c的取值范围为______．