初中数学二次函数在给定区间上的最值试题

如图所示的二次函数y=ax²+bx+c的图象中，刘星同学观察得出了下面四条信息：
（1）b²-4ac＞0；（2）c＞1；（3）2a-b＜0；（4）a+b+c＜0．你认为其中错误的有（ ）

A．2个

B．3个

C．4个

D．1个

将二次函数y=x²的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为（ ）

A．y=（x-1）^2+3	B．y=（x+1）^2+3
C．y=（x-1）^2-3	D．y=（x+1）^2-3

如图二次函数的图象经过A（－1，0）和B（3，0）两点，且交轴于点C．

（1）试确定、的值；
（2）若点M为此抛物线的顶点，求△MBC的面积．

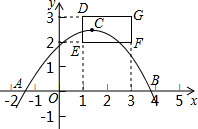
如图，抛物线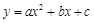与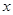轴的一个交点A在点（－2，0）和（1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则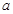的取值范围是               ．

已知抛物线（<0）过A（，0）、O（0，0）、B（，）、C（3，）四点．则        （用“＜”，“＞”或“=”填空）．

二次函数（a，b，c为常数，且）中的与的部分对应值如表：

	…	－1	0	1	3	…
	…	－1	3	5	3	…

下列结论：
（1）；
（2）当时，y的值随x值的增大而减小；
（3）3是方程 的一个根；
（4）当时，．
其中正确的个数为    （   ）
A．4个         B．3个         C．2个          D．1个 

下列四个函数图象中，当时，随的增大而增大的是 

在平面直角坐标系中，将二次函数y=2x²的图象向上平移2个单位，所得函数图象的解析式为

A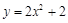．	B．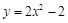
C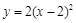．	D．

一个足球从地面上被踢出，它距地面高度y（米）可以用二次函数y=－4．9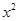+19．6x刻画，其中x（秒）表示足球被踢出后经过的时间．则足球被踢出后到离开地面达到最高点所用的时间是        秒．

已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列4个结论：
①abc＜0；②b＞a+c；③2a-b=0；④b²-4ac＜0．其中正确的结论个数是（   ）

A．1个

B．2个

C．3个

D．4个

某种商品的进价为40元/件，以获利不低于25%的价格销售时，商品的销售单价y（元/件）与销售数量x（件）（x是正整数）之间的关系如下表：

x（件）	…	5	10	15	20	…
y（元/ 件）	…	75	70	65	60	…

 
（1）由题意知商品的最低销售单价是      元，当销售单价不低于最低销售价时，y是x的一次函数．y与x的函数关系式是           ．
（2）当销售单价为多少元时，所获销售利润最大，最大利润是多少元？

如表，给出了一个二次函数的一些取值情况：

（1）请在坐标系中（答卷纸上）画出这个二次函数的图象；  
（2）根据图象写出：当0≤y<3时x的取值范围．

二次函数y=x²的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=x²的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积是______．

如图，正三角形ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C
的方向运动，到达点C时停止．设运动时间为x（秒），y＝PC²，则y关于x的函数的图象大致是（   ）

教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）间的
关系为，由此可知铅球推出的距离是（   ）

A．2m

B．8m

C．10m

D．12