初中数学一元二次方程的最值选择题

某果园2011年水果产量为100吨，2013年水果产量为144吨，求该果园水果产量的年平均增长率．设该果园水果产量的年平均增长率为x，则根据题意可列方程为（    ）

A．144（1-x）^2=100	B．100（1-x）^2=144
C．144（1+x）^2=100	D．100（1+x）^2=144

如果2 + 是方程x ²–cx + 1=0的一个根，那么c的值是（  ）

A．2－

B．－4

C．－4或2－

D．4

股票每天的涨、跌幅均不超过10%，即当涨了原价的10%后，便不能再张，叫做涨停；当跌了原价的10%后，便不能再跌，叫做跌停。已知一支股票某天跌停，之后两天时间又涨回到原价，若这两天此股票股价的平均增长率为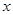，则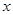满足的方程是

A．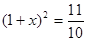

B．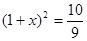

C．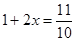

D．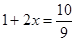

方程x²+3x-6=0与x²-6x+3=0所有根的乘积等于（    ）

A．-18

B．18

C．-3

D．3

若方程是关于x的一元二次方程，则的值是（   ）

A．＝±2

B．=2

C．=－2

D．≠±2

一元二次方程2x（x－3）＝5（x－3）的根为 （ ）

A．x＝

B．x＝3

C．x1＝3，x2＝－

D．x1＝3，x2＝

如图，在长为100米，宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644米²，则道路的宽应为多少米？设道路的宽为米，则可列方程为（   ）．

A．

B．

C．

D．．

某城市2011年已有绿化面积100公顷，经过两年绿化，绿化面积逐年增加，到2013底增加到144公顷，设绿化面积平均每年的增长率为，则根据题意可列方程为（   ）

A．

B．

C．

D．

已知一元二次方程用配方法解该方程，则配方后的方程是（   ）

A．	B．
C．	D．

已知m，n是关于x的一元二次方程x²﹣3x+a=0的两个解，若（m﹣1）（n﹣1）=﹣6，则a的值为（  ）

A．﹣10

B．4

C．﹣4

D．10

如图，公园要在一块长为100米，宽为 80 米的矩形场地上修建三条宽度相等的道路，其中两条 纵向，一条横向，横向道路与纵向道路垂直．剩余部分摆放不同的花卉，要使摆放花卉面积为7488m2，则道路的宽为多少米？设道路的宽为 x 米，则可列方程为（     ）

A．100×80-100x-80×2x="7488"

B．（100-2x）（80-x）="7488"

C．（100-2x）（80-x）+2x2="7488"

D．100x+80×2x=512

若实数、满足，则的值为（    ）

A．－2

B．4

C．4或－2

D．－4或2

已知二次函数y=x²﹣3x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x²﹣3x+m=0的两实数根是（ ）

A．x1=1，x2=﹣1

B．x1=1，x2=2

C．x1=1，x2=0

D．x1=1，x2=3

某校九年级（三）班学生毕业时，每个同学都将自己的相片向全班其他同学各送一张留作纪念，全班共送了2070张相片。如果全班有x名学生，根据题意，列出方程为（      ）

A．

B．

C．

D．

从正方形的铁皮上，截去2 cm宽的一条长方形，余下的长方形面积是48 cm²，则原来的正方形铁皮的面积是（    ）

A．68 cm^2

B．64 cm^2

C．9 cm^2

D．8 cm^2