浙江省诸暨市五校共进联考九年级上期中考试数学试卷
下列事件中,必然事件是( )
| A.掷一枚硬币,着地时反面向上 |
| B.星期天一定是晴天 |
| C.打开电视机,正在播放动画片 |
| D.在标准大气压下,水加热到100°会沸腾 |
二次函数y=2(x﹣1)2+3的图象的顶点坐标是( )
| A.(1,3) | B.(﹣1,3) | C.(1,﹣3) | D.(﹣1,﹣3) |
在Rt△ABC中, ∠C=Rt∠ ,AC=3cm, AB=5cm,若以C为圆心,4cm为半径画一个圆,则下列结论中,正确的是( )
| A.点A在圆C内,点B在圆C外 |
| B.点A在圆C外,点B在圆C内 |
| C.点A在圆C上,点B在圆C外 |
| D.点A在圆C内,点B在圆C上 |
下列各组数中的四条线段能成比例线段的是( )
| A.a=6,b=4,c=10,d=5 |
| B.a=3,b=7,c=2,d=9 |
| C.a=2,b=4,c=3,d=6 |
| D.a=4,b=11,c=3,d=2 |
若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-k的图象上的三点,则y1,y2,y3的大小关系是( )
| A.y1<y2<y3 | B.y2<y1<y3 | C.y3<y1<y2 | D.y1<y3<y2 |
某校九年级(三)班学生毕业时,每个同学都将自己的相片向全班其他同学各送一张留作纪念,全班共送了2070张相片。如果全班有x名学生,根据题意,列出方程为( )
A. |
B. |
C. |
D. |
如图所示的二次函数 的图象中,刘星同学观察得出了下面四条信息:(1)
的图象中,刘星同学观察得出了下面四条信息:(1) ;(2)c>1;(3)2a-b<0;(4)a+b+c<0。你认为其中错误的有( )
;(2)c>1;(3)2a-b<0;(4)a+b+c<0。你认为其中错误的有( )

| A.2个 | B.3个 | C.4个 | D.1个 |
如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE,BD的延长线交于点C。若CE=2,则图中阴影部分的面积是( )

A. B.
B. —
— C.
C. D.
D. —
—
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个

A.1 B.2 C.3 D.4
三张完全相同的卡片上分别写有函数 ,
, ,
, ,从中随机抽取一张,则所得卡片上函数的图象在第一象限内
,从中随机抽取一张,则所得卡片上函数的图象在第一象限内 随
随 的增大而增大的概率是 .
的增大而增大的概率是 .
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.

如图,一块等腰直角的三角板 ,在水平桌面上绕点
,在水平桌面上绕点 按顺时针方向旋转到
按顺时针方向旋转到 的位置,使
的位置,使 三点共线,那么旋转角度的大小为 .
三点共线,那么旋转角度的大小为 .

如果点P是线段AB的黄金分割点,且AP﹥PB,则下列命题,①AB2=AP•PB,②AP2=PB•AB,③BP2=AP•AB,④AP:AB=PB:AP,其中正确的是 (填序号).
如图,在平面直角坐标系中,长方形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为

已知一个口袋中装有4个只有颜色不同的球,其中3个白球,1个黑球.
(1)求从中随机抽取出一个黑球的概率是多少;
(2)若从口袋中摸出一个球,记下颜色后不放回,再摸出一个球。请列表或作出树状图,求两次都摸出白球的概率?
已知等腰三角形ABC,如图.
(1)用直尺和圆规作△ABC的外接圆;
(2)设△ABC的外接圆的圆心为O,若∠BOC=128°,求∠BAC的度数.
已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5).
(1)求该二次函数的解析式;
(2)求该二次函数图象与坐标轴的交点坐标;
如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2),将△OAB绕点O逆时针旋转90°后得△OA1B1.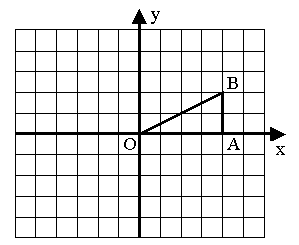
(1)在图中作出△OA1B1并直接写出A1,B1的坐标;
(2)求点B旋转到点B1所经过的路线长(结果保留π).
如图,AB为 的直径,AB=AC,BC交
的直径,AB=AC,BC交 于点D,AC交
于点D,AC交 于点E.
于点E.
(1)求证:BD=CD;
(2)若AB=8,∠BAC=45°,求阴影部分的面积.
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于65元,市场调查发现,若每箱以50元的价格出售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与涨价x(元/箱)之间的函数关系式;
(2)求当每箱苹果的销售价为多少元,批发商平均每天的销售利润W(元)可以获得最大?
如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD= ,求∠BAC的度数;
,求∠BAC的度数;
(2)若点E为 的中点,连接OE,CE.求证:CE平分∠OCD;
的中点,连接OE,CE.求证:CE平分∠OCD;
(3)在(1)的条件下,圆周上到直线AC距离为3的点有多少个?并说明理由.
如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得?QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线x=m(-1- <m<0)与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
<m<0)与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.

 的图象向右平移3个单位,再向上平移4个单位后,得到的新抛物线解析式是 .
的图象向右平移3个单位,再向上平移4个单位后,得到的新抛物线解析式是 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号