初中数学应用类问题解答题

奔跑的狗
苏步青是我国著名数学家、教育家，历任复旦大家教授、校长等职．1995年当选为中国科学院学部委员．苏步青的主要研究领域是微分几何学，他又是优秀的教学教育家，从事数学教学达60年，培养了大批数学人才．
一次在德国，苏步青与一位有名的数学家同乘电车时，这位数学家出了一道题目给苏教授解答．
这道题是：
甲乙两人同时从相距100千米的两地出发，相向而行，甲每小时走6千米，乙每小时走4千米，甲带了一只狗和他同时出发，狗以每小时10千米的速度向乙奔去，遇到乙即回头向甲奔去；遇到甲又回头向乙奔去，直到甲乙两人相遇时狗才停住．问这只狗共奔跑了多少千米路？

对这个问题，苏步青教授略加思索，就算出了正确的答案．请你也想一想，该怎么解答？

某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示，请在原图上利用尺规作图作出音乐喷泉M的位置，（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）

网格中有一个小甲虫（），它喜欢吃牛粪，它又会把吃剩的牛粪滚成牛粪球（）藏进仓库（）.规定向左为L，向右为R，向上为U，向下D，如：L1表示向左平移一格，D2表示向下平移2格.例如：要把左图中的所有的牛粪球推到最近的仓库里，可以编写程序：L1-R1-U2-D3-R2-U1，小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试，可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.（只需写出一种可行的程序即可）
               

将一个长方形纸片连续对折，对折的次数越多，折痕的条数也就越多，如第一次对折后，有1条折痕，第2次对折后，共有3条折痕。
（1）第3次对折后共有多少条折痕？第4次对折后呢？
（2）请找出折痕条数与对折次数的对应规律，写出对折n次后，折痕有多少条？

某市公交快速通道开通后，为响应市政府“绿色出行”的号召，家住新城的小王上班由自驾车改为乘坐公交车．已知小王家距上班地点18千米，他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米，他从家出发到达上班地点，乘公交车方式所用时间是自驾车方式所用时间的．小王用自驾车方式上班平均每小时行驶多少千米？

认真观察下图的四个图中阴影部分构成的图案，回答下列问题：
（1）利用所学知识，请写出这四个图案都具有的特征：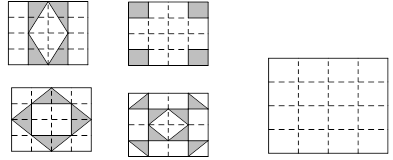

特征1：______________________________________；
特征2：______________________________________；
（2）请在备用图中设计你心目中最美丽的图案，使它也具备你所写的上述
特征．

检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发, 到收工时,行走记录为(单位:千米): +8、-9、+4、+7、-2、-10、+18、-3、+7、+5
回答下列问题:
(1)收工时在A地的哪边?距A地多少千米?
(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?

如图，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA＝PB．要求：尺规作图，并保留作图痕迹．

某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示，请在原图上利用尺规作图作出音乐喷泉M的位置，（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）

问题：如图1，在正方形ABCD内有一点P,PA=,PB=,PC=1，求∠BPC的角度．
分析：根据已知条件比较分散的特点，我们可以通过旋转变换，将分散的已知条件集中在一起，于是将△BPC绕点Ｂ逆时针旋转90^０，得到了△BP_１A（如图2），然后连接PP₁.

解决问题：请你通过计算求出图2中∠BPC的角度；
类比研究：如图3，若在正六边形ABCDEF内有一点P，且PA=,PB=4,PC=2．
（1）请你通过计算求出∠BPC的度数；
（2）直接写出正六边形ABCDEF的边长为              ．

阅读下列材料：小华遇到这样一个问题：已知：如图1，在△ABC中，AB=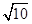，AC=，BC=2三边的长分别为，求∠A的正切值．

小华是这样解决问题的：如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．
（1）图2中与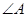相等的角为   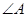      ， 的正切值为          ；
（2）参考小华解决问题的方法，利用图4中的正方形网格（每个小正方形的边长均为1）解决问题：如图3，在△GHK中，HK=2，H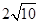G=，KG=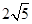，延长HK，求的度数．

璧山观音塘湿地公园是目前重庆最大的湿地公园，该公园以众多珍稀动植物和独特的灯光和喷泉，吸引着越来越多的游客前往游玩。为了应对游客在游玩过程中的意外伤害，公园决定在形状为如图所示的四边形中央广场内修建一个便民取药点，以便在里面配置各种应急药物。现要求该取药点离两个广场入口、的距离相等，且离观赏点的距离恰好等于、间的距离。请在原图上利用尺规作图作出取药点的位置。（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）

已知梯形ABCD，请使用无刻度直尺画图．

（1）在图1中画出一个与梯形ABCD面积相等，且以CD为边的三角形；
（2）图2中画一个与梯形ABCD面积相等，且以AB为边的平行四边形．

已知梯形中，∥，，，，.动点从点开始以的速度沿线段向点运动，动点从点开始以的速度沿线段向点运动.点、点分别从、两点同时出发，当其中一点停止时，另一点也随之停止。设运动时间为.
 
（1）求的长；
（2）以为圆心、长为半径的与直线相切时，求的值；
（3）是否存在的值，使得以为圆心、长为半径的与以为圆心、长为半径的相切？若存在，求出的值；若不存在，请说明理由.

2004年12月28日，我国第一条城际铁路-----合宁铁路（合肥至南京）正式开工建设，建成后，合肥至南京的铁路运行里程将由目前的缩短至，设计时速是现行时速的倍。旅客列车运行时间将因此缩短约，求合宁铁路的设计时速