初中数学应用类问题解答题

某市计划在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A、B的距离相等，且到广场管理处C的距离等于A和B之间距离的一半，A、B、C的位置如图所示，请在原图上利用尺规作图作出音乐喷泉M的位置，（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）

某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．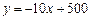
设李明每月获得利润为W（元），当销售单价定为多少元时，每月可获得最大利润？
如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）

已知某市居民生活用电基本价格为每度0.45元，若每月用电量超过a度，超过部分按基本电价的70%收费。
（1）某户5月份用电84度，共缴电费30.72元，求a的值。
（2）若该户六月份的电费平均每度为0.36元，求6月份共用多少度电？应交电费多少元？

随着人民生活水平的不断提高，我市家庭轿车的拥有量逐年增加.据统计，某小区2007年底拥有家庭轿车64辆，2009年底家庭轿车的拥有量达到100辆.若该小区2007年底到2010年底家庭轿车拥有量的年平均增长率都相同，求该小区到2010年底家庭轿车将达到多少辆？

问题：如图1，在正方形ABCD内有一点P,PA=,PB=,PC=1，求∠BPC的角度．
分析：根据已知条件比较分散的特点，我们可以通过旋转变换，将分散的已知条件集中在一起，于是将△BPC绕点Ｂ逆时针旋转90^０，得到了△BP_１A（如图2），然后连接PP₁.

解决问题：请你通过计算求出图2中∠BPC的角度；
类比研究：如图3，若在正六边形ABCDEF内有一点P，且PA=,PB=4,PC=2．
（1）请你通过计算求出∠BPC的度数；
（2）直接写出正六边形ABCDEF的边长为              ．

当a = -2，b=1时，求两个代数式（a+b）²与a²+2ab+b²的值
当a =-2，b= -3时，再求以上两个代数式的值；
你能从上面的计算结果中，发现上面有什么结论？
结论是：                                  ；
利用你发现的结论，求：1965²+1965×70+35²的值．

初一学生王马虎同学在做作业时，不慎将墨水瓶打翻，使一道作业只能看到：甲、乙两地相距160千米，摩托车的速度为45千米/时，运货汽车的速度为35千米/时，______________________________？请你将这道作业题补充完整并列出方程解答。

（本题共4分）图1是一个三角形，分别连接这个三角形三边的中点得到图②；再分别连接图②中间小三角形三边的中点，得到图③.
                   

	①		②		③

 

⑴图②有_____个三角形；图③有_____个三角形.
⑵按上面的方法继续下去，第 个图形中有多少个三角形？（用含有 的式子表示结论）数值。

璧山观音塘湿地公园是目前重庆最大的湿地公园，该公园以众多珍稀动植物和独特的灯光和喷泉，吸引着越来越多的游客前往游玩。为了应对游客在游玩过程中的意外伤害，公园决定在形状为如图所示的四边形中央广场内修建一个便民取药点，以便在里面配置各种应急药物。现要求该取药点离两个广场入口、的距离相等，且离观赏点的距离恰好等于、间的距离。请在原图上利用尺规作图作出取药点的位置。（要求：不写已知、求作、作法和结论，保留作图痕迹，必须用铅笔作图）

某地电话拨号上网有两种收费方式，用户可以任意选择其中一种：第一种是计时制，0.05元／分； 第二种是包月制，69元／月（限一部个人住宅电话上网）．此外，每一种上网方式都得加收通讯费0.02元／分．
（1）若小明家今年三月份上网的时间为小时，请你分别写出两种收费方式下小明家应该支付的费用；
（2）若小明估计自家一个月内上网的时间为20小时，你认为采用哪种方式较为合算？

阅读下列材料：小华遇到这样一个问题：已知：如图1，在△ABC中，AB=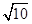，AC=，BC=2三边的长分别为，求∠A的正切值．

小华是这样解决问题的：如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．
（1）图2中与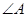相等的角为   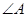      ， 的正切值为          ；
（2）参考小华解决问题的方法，利用图4中的正方形网格（每个小正方形的边长均为1）解决问题：如图3，在△GHK中，HK=2，H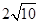G=，KG=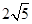，延长HK，求的度数．

已知梯形ABCD，请使用无刻度直尺画图．

（1）在图1中画出一个与梯形ABCD面积相等，且以CD为边的三角形；
（2）图2中画一个与梯形ABCD面积相等，且以AB为边的平行四边形．

已知梯形中，∥，，，，.动点从点开始以的速度沿线段向点运动，动点从点开始以的速度沿线段向点运动.点、点分别从、两点同时出发，当其中一点停止时，另一点也随之停止。设运动时间为.
 
（1）求的长；
（2）以为圆心、长为半径的与直线相切时，求的值；
（3）是否存在的值，使得以为圆心、长为半径的与以为圆心、长为半径的相切？若存在，求出的值；若不存在，请说明理由.

2004年12月28日，我国第一条城际铁路-----合宁铁路（合肥至南京）正式开工建设，建成后，合肥至南京的铁路运行里程将由目前的缩短至，设计时速是现行时速的倍。旅客列车运行时间将因此缩短约，求合宁铁路的设计时速

列方程解应用题
甲、乙两站相距360千米，一列慢车从甲站开出，每小时行50千米，一列快车从乙站开出，每小时行70千米，两车同时开出，相向而行，多长时间相遇？