初中数学应用类问题解答题

图形的操作过程（本题中四个矩形的水平方向的边长均为a，竖直方向的边长均b）：

●在图1中，将线段A1A2向右平移1个单位到B1B2，得到封闭图形A1A2B2B1（即阴影部分）；
●在图2中，将折线A1A2A3向右平移1个单位到B1B2B3，得到封闭图形A1A2A3B3B2B1（即阴影部分）．
（1）在图3中，请你类似地画一条有两个折点的线，同样向右平移1个单位，从而得到一个封闭图形，并用斜线画出阴影；
（2）请你分别写出上述三个图形中除去阴影部分后剩余部分的面积：
S1＝__________，S2＝__________，S3＝__________．
（3）联想与探索
 
如上图，在一块矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示的草场地面积是多少？并说明你的猜想是正确的．

小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示。根据图中的数据（单位：m），解答下列问题：

①用含、的代数式表示地面总面积；
②当，时，若铺1m²地砖的平均费用为80元，那么铺地砖的总费用为多元？

如图，某校有一块长为(3a＋b)米，宽为(2a+b)米的长方形地块，学校计划将阴影部分进行绿化，中间将修建一座雕像.

(1) 用含a、b的代数式表示绿化面积；
(2) 求出当a=3米,b=2米时的绿化面积．

如图，图中的物体由7块相同的立方体组成，请画出它的三视图。

某高铁工程即将动工,工程需要测量某一条河的宽度.如图，一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向，测量员从A点开始沿岸边向正东方向前进100米到达点C处，测得标杆B在北偏西280处.求河宽AB.（结果精确到1米）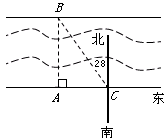

检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发, 到收工时,行走记录为(单位:千米): +8、-9、+4、+7、-2、-10、+18、-3、+7、+5
回答下列问题:
(1)收工时在A地的哪边?距A地多少千米?
(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?

如图，小明欲利用测角仪测量树的高度．已知他离树的水平距离BC为10m，测角仪的高度CD为1.5m，测得树顶A的仰角为33°．求树的高度AB．
（参考数据：sin33°≈0.54，cos33°≈0.84，tan33°≈0.65）

．某人2008年初投资120万元于股市，由于无暇操作，第一年的亏损率为20%，以后其亏损率有所变化，至2011年初其股票市值仅为77.76万元，求此人的股票在第二年、第三年平均每年的亏损率.

(10分）某人在银行的信用卡存入2万元，每次取出50元，若卡内余额为 y（元），取钱的次数为x.(利息忽略不计）
（1）、写出y与x之间的函数关系式，并求出自变量的取值范围？
（2）、取多少次钱以后，余额为原存款的四分之一？

阅读下列材料：小华遇到这样一个问题：已知：如图1，在△ABC中，AB=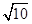，AC=，BC=2三边的长分别为，求∠A的正切值．

小华是这样解决问题的：如图2所示，先在一个正方形网格（每个小正方形的边长均为1）中画出格点△ABC（△ABC三个顶点都在小正方形的顶点处），然后在这个正方形网格中再画一个和△ABC相似的格点△DEF，从而使问题得解．
（1）图2中与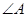相等的角为   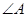      ， 的正切值为          ；
（2）参考小华解决问题的方法，利用图4中的正方形网格（每个小正方形的边长均为1）解决问题：如图3，在△GHK中，HK=2，H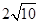G=，KG=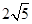，延长HK，求的度数．

已知梯形ABCD，请使用无刻度直尺画图．

（1）在图1中画出一个与梯形ABCD面积相等，且以CD为边的三角形；
（2）图2中画一个与梯形ABCD面积相等，且以AB为边的平行四边形．

已知梯形中，∥，，，，.动点从点开始以的速度沿线段向点运动，动点从点开始以的速度沿线段向点运动.点、点分别从、两点同时出发，当其中一点停止时，另一点也随之停止。设运动时间为.
 
（1）求的长；
（2）以为圆心、长为半径的与直线相切时，求的值；
（3）是否存在的值，使得以为圆心、长为半径的与以为圆心、长为半径的相切？若存在，求出的值；若不存在，请说明理由.

2004年12月28日，我国第一条城际铁路-----合宁铁路（合肥至南京）正式开工建设，建成后，合肥至南京的铁路运行里程将由目前的缩短至，设计时速是现行时速的倍。旅客列车运行时间将因此缩短约，求合宁铁路的设计时速

列方程解应用题
甲、乙两站相距360千米，一列慢车从甲站开出，每小时行50千米，一列快车从乙站开出，每小时行70千米，两车同时开出，相向而行，多长时间相遇？

如图，在直角坐标系中，已知点P0的坐标为(1，0)，将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此下去，得到线段OP3，OP4，…，OPn(n为正整数)

(1)求点P6的坐标；
(2)求△P5OP6的面积；
(3)我们规定：把点Pn(xn，yn)(n=0，1，2，3…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|，|yn|)称之为点Pn的“绝对坐标”．根据图中点Pn的分布规律，请你猜想点Pn的“绝对坐标”，并写出来