福建省惠安县初二上学期末数学卷
图形的操作过程(本题中四个矩形的水平方向的边长均为a,竖直方向的边长均b): 
●在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);
●在图2中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1=__________,S2=__________,S3=__________.
(3)联想与探索
如上图,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草场地面积是多少?并说明你的猜想是正确的.
已知菱形 的对角线
的对角线 和
和 相交于点
相交于点 ,
, ,
, ,
,

(1)菱形的对角线 和
和 具有怎样的位置关系?
具有怎样的位置关系?
(2)若沿两条对角线把菱形剪开,分成四个三角形,利用这四个三角形可拼成一个可以证明勾股定理的图形.请你画出示意图,并证明勾股定理.
(3)若 ,
, ,求
,求
①菱形的边长和菱形的面积.(直接写出结论)
②求菱形的高.(直接写出结论)
下列说法正确的是( )
| A.“明天降雨的概率是80%”表示明天有80%的时间降雨 |
| B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币10次有5次出现正面朝上 |
| C.“彩票中奖的概率是1%”表示买100张彩票一定会中奖 |
| D.抛掷一枚图钉,针尖触地和针尖朝上的概率不相等 |
如图,小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则球拍拍球的高度 应为( )
应为( )
| A.2.7米 | B.1.8米 | C.0.9米 | D.6米 |
在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( )
| A.9.5 | B.10.5 | C.11 | D.15.5 |
如图是一个质量均匀的圆形转盘,圆盘被等分成黑、红、白三部分,轻轻转动圆盘,则指针恰好指在红色部分的概率是__________
据某市交通部门统计,该市2008年底全市汽车拥有量为150万辆,而截止到2010年底,全市的汽车拥有量已达216万辆.设这两年中汽车平均每年增长的百分率为 ,则可列方程为:
,则可列方程为:
如图所示,已知:点 ,
, ,
,  .在
.在 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在 轴上,另一个顶点在
轴上,另一个顶点在 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个 ,第2个
,第2个 ,第3个
,第3个 ,…,则①
,…,则① = 度;②
= 度;② =
=
如图, 与
与 是位似图形,且顶点都在格点上.
是位似图形,且顶点都在格点上.
(1) 在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)△ABC与△A/B/C/的相似比为
某高铁工程即将动工,工程需要测量某一条河的宽度.如图,一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得标杆B在北偏西280处.求河宽AB.(结果精确到1米)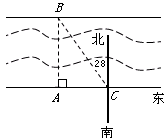
如图,AC平分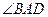 ,
,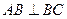 ,垂足为点B,
,垂足为点B,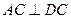 ,垂足为点C.
,垂足为点C.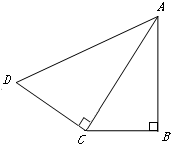
(1)请你判断△ABC与△ACD是否相似,并说明理由;
(2)若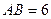 ,
,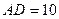 ,求AC的长.
,求AC的长.
在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,且整体图案成轴对称图形.下面是小华、小芳与小明的设计方案.
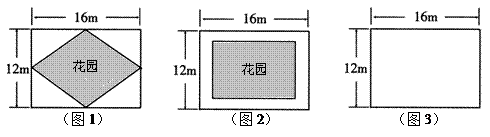
请你根据以上的对话,完成下列问题.
(1)你认为小华所设计的花园的形状是 ,整个设计图案共有 条对称轴;
(2)请你帮助小芳计算出道路的宽度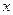 的值;
的值;
(3)请你根据小明的设计方案在图3中画出符合设计条件的草图,然后根据你所画的草图求出该等腰梯形的上底和下底的长.
将图(甲)中阴影部分的小长方形变换到图(乙)位置,根据两个图形的面积关系得到的数学公式是( )
A. |
B. |
C. |
D. |
如图(甲)所示的四张牌,若只将其中一张牌旋转180°后得到图(乙),则旋转的牌是( )
| A.第一张 | B.第二张 | C.第三张 | D.第四张 |
如图,点P为□ABCD的边CD上一点,若△PAB、△PCD和△PBC的面积分别为
s1、s2和s3,则它们之间的大小关系是( )
 A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
如图,正方形网格中 ,每小格正方形边长为1,则格点△ABC中,边长为无理数的边数有( )
| A.0条 | B.1条 | C.2条 | D.3条 |
如图(甲),在俄罗斯方块游戏中,上方小方块可先 (填“顺”或“逆”)时针旋转 度,再向 (填左或右)平移至边格,然后让它自己往下移动,最终拼成一个完整的图案如图(乙),使其自动消失.
如图,网格中有一个四边形和两个三角形.
⑴ 请你分别画出三个图形关于点O的中心对称图形;
⑵ 将⑴中画出的图形与原图形看成一个整体图形,请你写出这个整体图形对称轴的
条数是 ;这个整体图形至少旋转 度后才能与自身重合.
如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.
(1) 用含a、b的代数式表示绿化面积;
(2) 求出当a=3米,b=2米时的绿化面积.
如图,一艘渔政船从小岛A处出发,向正北方向以每小时20海里的速度行驶了1.5小时到达B处执行任务,再向正东方向以相同的速度行驶了2小时到达C处继续执行任务,然后以相同的速度直接从C处返回A处.
(1)分别求AB、 BC的长;
(2)问返回时比出去时节省了多少时间?
如图,在梯形ABCD中,AD∥BC,AB="DC" ,过点D作DE∥AB 交BC于点E.
(1) 请你判断四边形ABED的形状,并说明理由;
(2) 当△DEC为等边三角形时,
① 求∠B的度数;
② 若AD=4,DC=3,求等腰梯形ABCD的周长.
如图①,矩形纸片ABCD的边长分别为a、b(a<b),点M、N分别为边AD、BC上两点(点A、C除外),连结MN.
(1)如图②,分别沿ME、NF将MN两侧纸片折叠,使点A、C分别落在MN上的A’、C’处,直接写出ME与FN的位置关系;
(2)如图③,当MN⊥BC时,仍按(1)中的方式折叠,请求出四边形A’EBN与四边形C’FDM
的周长(用含a的代数式表示),并判断四边形A’EBN与四边形C’FDM周长之间的数量关系;
(3)如图④,若对角线BD与MN交于点O,分别沿BM、DN沿ME、NF将MN两侧纸片折叠,折叠后,点A、C恰好都落在点O处,并且得到的四边形BNDM是菱形,请你探索a、b之间的数量关系;
(4)在(3)情况下,当a= 时,求菱形BNDM的面积.
时,求菱形BNDM的面积.
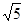
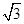

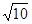
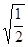
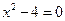 的解是( )
的解是( )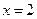
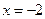
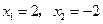
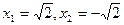
 ,下列配方正确的是( )
,下列配方正确的是( )



 中,∠C=90°,BC=3cm,AC=4cm,则
中,∠C=90°,BC=3cm,AC=4cm,则 的值为( ).
的值为( ).



 ____________时,二次根式
____________时,二次根式 在实数范围内有意义
在实数范围内有意义 =" "
=" " ,则
,则 ____________
____________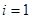 ,则该坡的坡角
,则该坡的坡角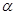 =
= 
 是方程
是方程 的一个实数根,则
的一个实数根,则 的值是
的值是  在边
在边 上,
上, ,连接
,连接 交
交 于点
于点 ,则
,则 的面积与
的面积与 的面积之比为_______
的面积之比为_______
 ②
②
 . ②
. ②
 ,其中a=3,b=
,其中a=3,b=
 2
2


 =
=
 是一个完全平方式,则常数k的值为( )
是一个完全平方式,则常数k的值为( ) 的结果是___________
的结果是___________ ≌△
≌△ , 若∠
, 若∠ =60°,∠
=60°,∠ =20°,
=20°, = °
= °



 = .
= . BC,E是垂足,如果∠B=50°,那么∠D、
BC,E是垂足,如果∠B=50°,那么∠D、 
 粤公网安备 44130202000953号
粤公网安备 44130202000953号