如图所示，已知在直角梯形
中，
轴于点
．动点
从
点出发，沿
轴正方向以每秒1个单位长度的速度移动．过点作
垂直于直线
，垂足为
．设点移动的时间为
秒（
），
与直角梯形重叠部分的面积为
．
（1）求经过
三点的抛物线解析式；
（2）求与的函数关系式；
（3）将绕着点顺时针旋转
，是否存在，使得的顶点或在抛物线上？若存在，直接写出的值；若不存在，请说明理由．
安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF所在直线相交与水箱横截面⊙O的圆心O,⊙O的半径为0.2m,AO与屋面AB的夹角为32°，与铅垂线OD的夹角为40°，BF⊥AB于B，OD⊥AD于D，AB＝2m,求屋面AB的坡度和支架BF的长.
(参考数据：
)
如图，在直角坐
标系中，已知点P0的坐标
为(1，0)，将线段OP0按逆时针方向旋转45°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转45°，长度伸长为OP1的2倍，得到线段OP2；如此
下去，得到线段OP3，OP4，…，OPn(n为正整数)
(1)求点P6的坐标；
(2)求△P5OP6的面积；
(3)我们规定：把点Pn(xn，yn)(n=0，1，2，3…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|，|yn|)称之为点Pn的“绝对坐标”．根据图中点Pn的分布规律，请你猜想点Pn的“绝对坐标”，并写出来
一宾馆准备在大厅的主楼梯上铺设一种红地毯，已知地毯40元/米2，主楼梯的宽为2米，其侧面如图所示，则地毯至少需要多少元？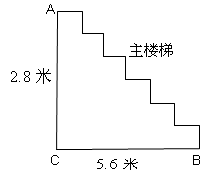
已知一个三角形的两边分别为
，这两边的夹角为
，请用尺规作图法作出这个三角形．(要求：写出已知、求作，保留作图痕迹，不写作法，最后要作答)
图案设计：正方形绿化场地拟种植两种不同颜色的花卉，要求种植的花卉
能组成轴对称或中心对称图案．下面是三种不同设计方案中的一部分，请把图①、图②
补成既是轴对称图形，又是中心对称图形，并画出一条对称轴；把图③补成只是中心对称图形，并把中心标上字母P。（在你所设计的图案中用阴影部分和非阴影部分表示两种不同颜色的花卉。）
如图，小明在十月一日到公园放风筝，风筝飞到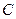
处时的线长为20米，此时小明正好站在A处，并测得
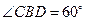，牵引底端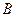
离地面1.5米，求此时风筝离地面的高度．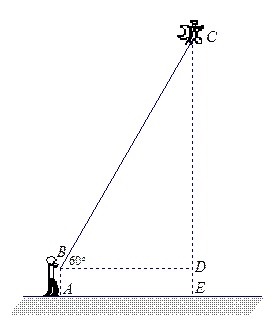
某天，一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40公斤到菜市场去卖，西红柿和豆角这天的批发价与零售价如下表所示：
| 品名 |
西红柿 |
豆角 |
| 批发价（单位：元/公斤） |
1.2 |
1.6 |
| 零售价（单位：元/公斤） |
1.8 |
2.5 |
问：（1）该经营户当天在蔬菜批发市场批了西红柿和豆角各多少公斤？
（2）他当天卖完这些西红柿和豆角能赚多少钱？
下面是按一定规律排列的一列数：
第1个数：
；
第2个数：
；
第3个数：
；
……
第
个数：
．
那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
| A．第10个数 | B．第11个数 | C．第12个数 | D．第13个数 |
3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．
4．已知：
，
，求ab的值。
5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解
如图7，利用一面墙（墙的最大可用长度为10米），用长为24米的篱笆围成中间隔有一道篱笆的长方形花圃ABCD．如果要在两个矩形的BC一边各开一个1.5米宽的门（做门材料不占用篱笆
），且花圃的总面积为54
平方米，那么花圃的宽AB应为多少米？
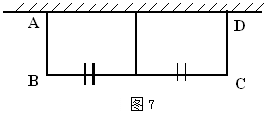
如图5，在下面由火柴棒拼出的一系列的图形中，第n个图形由n个正方形组成．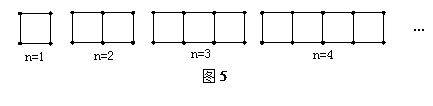
（1）第2个图形中，火柴棒的根数是__________；
（2）第3个图形中，火柴棒的根数是__________；
（3）第n个图形中，火柴棒的根数是__________；
（4）按此规律，拼到第几个图形时，所用的火柴数量是2011根
当温度上升1℃时，某种金属丝伸长0.002mm；当温度下降1℃时
，金属丝就缩短0.002mm.把15℃的这种金属丝加热到50℃，再冷却降温到8℃，金属丝最后的长度比原来的长度伸长多少？
如图，A、B是两个蓄水池，都在河边
的同侧，为了方便灌溉农作物，要在河边建一个抽水站，将河水送到A、B两地。问该站建在河边什么地方，可使所修
的渠道最短？试
在图中确定该点。（保留作图痕迹）
一张长方形的餐桌可以坐6个人，按照下图的方式摆放餐桌和椅子：
（1）观察表中数据规律填表：
| 餐桌张数 |
1 |
2 |
3 |
4 |
… n |
| 可坐人数 |
6 |
8 |
10 |
|
|
（2）一家酒楼，按上图的方式拼桌，要使拼成的一张大餐桌刚好能坐160人，请问需几张餐桌拼成一张大餐桌？
（3）若酒店有240人来一起就餐，要拼成一张大餐桌,怎样拼桌需要的餐桌最少？最少要用多少张？
粤公网安备 44130202000953号