下面是按一定规律排列的一列数：
第1个数：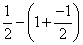
；
第2个数：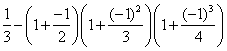
；
第3个数：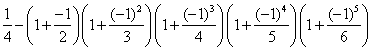
；
……
第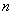
个数：
．
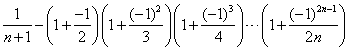那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）
| A．第10个数 | B．第11个数 | C．第12个数 | D．第13个数 |
3．已知：a为有理数，a3+a2+a+1=0，求1+a+a2+a3+…+a2012的值．
4．已知：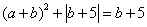
，
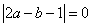，求ab的值。
5．当整数k为何值时，方程9x-3=kx+14有正整数解？并求出正整数解
相关试题
（本题5分）在“六一国际儿童节”来临之际，某校开展了向山区“希望小学”捐赠图书活动.全校1000名学生每人都捐赠了一定数量的图书，已知各年级人数分布的扇形统计图如图⑴所示.学校为了了解各年级捐赠图书情况，从各年级中随机抽查了部分学生，进行捐赠图书情况的统计，绘制成如图⑵的频数分布直方图.
根据以上信息解答下列问题：
（1）人均捐赠图书最多的是 年级；
（2）估计九年级学生共捐赠图书多少册?
（3）全校大约共捐赠图书多少册?
，再选一个你认为合适的数作为a的值代入求值
相关知识点
推荐套卷
粤公网安备 44130202000953号