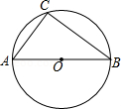
如图, 是 的外接圆, 是 的直径, .
(1)利用尺规,作 的平分线,交 于点 ;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 , ,若 ,求 的度数;
(3)在(2)的条件下, 交 于点 ,求由线段 , , 所围成区域的面积.(其中 表示劣弧,结果保留 和根号)
相关知识点
推荐套卷
如图, 是 的外接圆, 是 的直径, .
(1)利用尺规,作 的平分线,交 于点 ;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接 , ,若 ,求 的度数;
(3)在(2)的条件下, 交 于点 ,求由线段 , , 所围成区域的面积.(其中 表示劣弧,结果保留 和根号)
