如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断 AB、AE的数量关系,并说明理由;
AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,
sin76°≈0.97,cos76°≈0.24)
某城市进行旧城区人行道的路面翻新,准备对地面密铺彩色地砖,有人提出了以下 种地砖的形状供设计选用.其中不能进行密铺的地砖的形状是
种地砖的形状供设计选用.其中不能进行密铺的地砖的形状是
| A.正三角形 | B.正四边形 | C.正五边形 | D.正六边形 |
如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…依此类推,则第n个正方形的边长为______________
在同一时刻,两根长度不等的杆子置于阳光之下,但它们的影长相等,这两根杆子的相对位置是______________
(本小题满分12分)
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x(单位:分)如图2所示.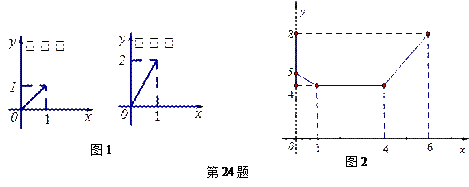
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
某宾馆有若干间住房,住宿记录提供了如下信息:①10月5日全部住满,一天住宿费收入为12000元;②10月6日有20间房空着,一天住宿费收入为9600元;③该宾馆每间房每天收费标准相同.
(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
(2)10月份以后,通过市场调查发现,每间住房每天的定价每增加10元,该宾馆的所有房间就会有5个房间空闲;己知该宾馆空闲房间每天每间支出费用10元,有游客居住房间每天每间支出费用20元,问房价定为多少元时,该宾馆一天的利润为11000元?
(利润=住宿费收入-支出费用)
(7分)
近年来,国家实施“村村通”工程和农村医疗卫生改革,某县计划在张村、李村之间建一座定点医疗站P,张、李两村座落在两相交公路内(如图所示)。医疗站必须满足下列条件:①使其到两公路距离相等,②到张、李两村的距离也相等,请你通过作图确定P点的位置(不写作法,保留作图痕迹)
有个数值转换器,原理如图所示,当输入x为27时,输出y的值是
| A.3 | B. |
C. |
D. |
如图,将一张正方形纸片剪成四个小正方形,如图(1);然后再将其中的一个正方形剪成四个小正方形,此时共有7个正方形,如图(2);再将其中的一个正方形剪成四个小正方形,此时共有10个正方形,如图(3).按此操作继续下去… ……
……
(1)根据以上操作方法,请你填写下表:
操作次数 |
1 |
2 |
3 |
4 |
5 |
… |
| 正方形的个数S |
4 |
7 |
10 |
|
|
… |
(2)用代数式表示正方形的个数S和操作次数 之间的关系;
之间的关系; (3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.
(3)按此方法操作下去,正方形的个数能否为2010个?若能,请说出是经过多少次操作后得到的;若不能,请说明理由.
某地有两座工厂和两条交叉的公路,图中点M、N表示工厂,OA、OB表示公路,现计划修建一座物资仓库,希望仓库到两工厂的距离相同,到两条公路的的距离相同,你能确定出仓库P应该建在什么位置吗?请在图中画出你的设计。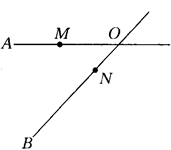
(尺规作图,不写作法,保留作图痕迹)
小明设计了一个关于实数运算的程序,输入一个数后,输出的数总是比该数的平方小1,小明按照此程序输入 后,输出的结果应为______
后,输出的结果应为______
小丽从镜子中看到镜子对面墙上挂着的电子表,其计数为1:1,则电子表的实际时刻是____
某饭店一周中,每天的盈亏情况如下,(盈余为正)
128, ―27元,―13元,22元,―17元,33元,76元
这个饭店一周总的盈亏情况如何?
(满分8分)在国家的宏观调控下,某市的商品房成交价由今年3月分的14000元/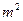 下降到5月份的12600元/
下降到5月份的12600元/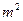
(1)问4、5两月平均每月降价的百分率是多少?(参考数据: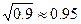 )
)
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成 交均价是否会跌破10000元/
交均价是否会跌破10000元/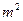 ?请说明理由。
?请说明理由。