宁夏银川市初三上学期期末数学卷
如图,⊙O的半径为5cm, AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.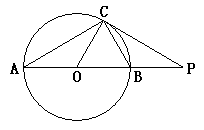
(1)求证:PC是⊙O的切线;
(2)求线段BC的长度.
如图①,直线 与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且
与x轴、y轴分别交于B、C两点,点A在x轴负半轴上,且 ,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
,抛物线经过A、B、C三点,D为线段AB中点,点P(m,n)是该抛物线上的一个动点(其中m>0,n<0),连接DP交BC于点E.
(1)写出A、B、C三点的坐标,并求抛物线的解析式;
(2) 当△BDE是等腰三角形时,直接写出此时点E的坐标;
(3)连结PC、PB,△PBC是否有最大面积?若有,求出△PBC的最大面积和此时P点的坐标;若没有,请说明理由。
如图,△OCA≌△OBD,C和B,A和D是对应顶点,如果OA=6,AC=5,OC=4,那么DB的长是( )
| A.4 | B.5 | C.6 | D.无法确定 |
下图是屋架设计图的一部分,立柱BC垂直于横梁AC,AB=8m,∠A=30°,则立柱BC的长度为( )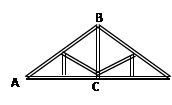
| A.4m | B.8m | C.10m | D.16m |
如图,已知点P在∠AOB的平分线OC上,PF⊥OA,PE⊥OB,若PE=6,则PF的长为( )
| A.2 | B.4 | C.6 | D.8 |
已知等腰三角形的一个角是80°,则它的另外两个角分别是( )
| A.50°,50° | B.20°,80° |
| C.50°,50°或20°,80° | D.80°,80° |
如图, △ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是________ cm
下面的图象反映的过程是:
张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回
家.其中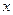 表示时间,
表示时间,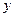 表示张强离家的距离.
表示张强离家的距离.
根据图象回答下列问题:
(1)体育场离张强家________千米;
(2)体育场离文具店________千米,张强在文具店停留了________分;
(3)请计算:张强从文具店回家的平均速度是多少?
下面是某同学对多项式 进行因式分解的过程.
进行因式分解的过程.
解:设
原式= (第一步)
(第一步)
= (第二步)
(第二步)
= (第三步)
(第三步)
= (第四步)
(第四步)
请问:(1)该同学因式分解的结果是否彻底?____________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果________________________________
(2)请你模仿以上方法尝试对多项式 进行因式分解.
进行因式分解.
一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量 (L)随行驶里程
(L)随行驶里程 (km)的增加而减少,平均耗油量为0.11L/km.
(km)的增加而减少,平均耗油量为0.11L/km.
(1)写出表示 与
与 的函数关系式.
的函数关系式.
(2)指出自变量 的取值范围.
的取值范围.
(3)汽车行驶200km时,油箱中还有多少汽油?
某学校计划组织240名师生集体外出活动,计划租用甲、乙两种型号客车共6辆.已知甲、乙两种大客车的载客量和租金如下表,设租用甲种客车 辆,租车总费用
辆,租车总费用 元.
元.
(1)求出表示 与
与 的函数关系式.
的函数关系式.
(2)给出最节省费用的租车方案;最节省费用为多少?
已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.
求证:(1)AE=DB;
(2)△CMN为等边三角形.
某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为 ( )
| A.6米 | B.7米 | C.8.5米 | D.9米 |
关于频率和概率的关系,下列说法正确的是( ).
| A.频率等于概率 |
| B.当实验次数很大时,频率稳定在概率附近 |
| C.当实验次数很大时,概率稳定在频率附近 |
| D.实验得到的频率与概率不可能相等 |
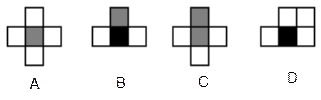
如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )
在平面直角坐标系中,反比例函数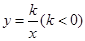 图象的两支曲线分别在( ).
图象的两支曲线分别在( ).
| A.第一、三象限; | B.第二、四象限; | C.第一、二象限; | D.第三、四象限 |
如图,在△ABC中,CD是∠ACB的平分线,∠A = 80°,∠ACB = 60°,那么∠BDC =( )
| A.80° | B.90° | C.100° | D.110° |
已知四边形 ,有以下四个条件:①
,有以下四个条件:① ;②
;② ;③
;③ ;④
;④ .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形 成为平行四边形的选法种数共有( )
成为平行四边形的选法种数共有( )
| A.6种 | B.5种 | C.4种 | D.3种 |
为了测量水塔的高度,取一根竹杆放在阳光下,已知2米长的竹杆投影长为1.5米,在同一时刻测得水塔的投影长为30米,则水塔高为_______米.
如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为4的概率是 
如图,点B、D、C、F在一条直线上,且BC = FD,AB = EF.
(1)请你只添加一个条件(不加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.
如图,楼房和旗杆在路灯下的影子如图所示.
(1)试确定路灯灯炮的位置;
(2)再作出小树在路灯下的影子.(用线 段表示,不写作法,保留作图痕迹)
段表示,不写作法,保留作图痕迹)
某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降低50 元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
元,平均每天就能多售出4台,商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
如图,A信封中装有两张卡片,卡片上分别写着7cm、3cm;B信封中装有三张卡片,卡片上分别写着2cm、4cm、6cm;信封外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从两个信封中各取出一张卡片,与信封外的卡片放在一起,用卡片上标明的数量分别作三条线段的长度.用画树状图法,求这三条线段能组成三角 形的概率.
形的概率.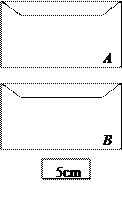
如图,在□ABCD中,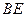 平分
平分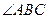 交
交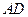 于点
于点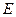 ,
,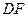 平分
平分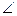
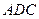 交
交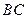 于点
于点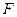 .
.
求证:(1)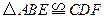 ;
;
(2)若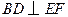 ,则判断四边形
,则判断四边形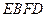 是什么特殊四边形,请证明你的结论.
是什么特殊四边形,请证明你的结论.
某中学计划对本校七年级10个班的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴趣小组,小明从每个班中随机抽取5名学生进行问卷调查,并将统计结果制成如下所示的表和图.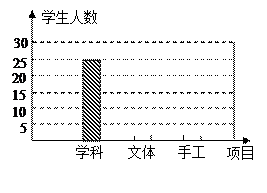
| 兴趣小组 |
划 记 |
频数 |
百分比 |
| 学科 |
正正正正正 |
25 |
|
| 文体 |
正正 |
|
|
| 手工 |
正正正 |
|
|
| 合计 |
50 |
50 |
|
(1)请将统计表、统计图补充完整;
(2)请以小明的统计结果来估计该校七年级480名学生参加各个项目的人数.
如图,点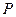 的坐标为(2,
的坐标为(2,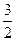 ),过点
),过点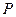 作
作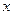 轴的平行线交
轴的平行线交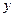 轴于点
轴于点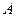 ,交双曲线
,交双曲线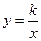 (
(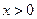 )于点
)于点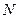 ,作
,作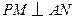 交双曲线
交双曲线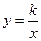 (
(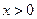 )于点
)于点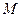 ,连结
,连结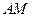 .已知
.已知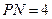 .
.
(1)求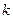 的值.
的值.
(2)求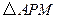 的周长
的周长
如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙-2,-5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D. 
(1) 求反比例函数 和一次函数
和一次函数 的表达式;
的表达式;
(2) 连接OA,OC.求△AOC的面积.








 的图象不经过( )
的图象不经过( ) 的相反数是__________
的相反数是__________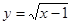 中,自变量
中,自变量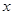 的取值范围是________
的取值范围是________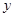 值随
值随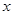 值的增大而减小:____
值的增大而减小:____ =_________
=_________

 的解是 ( )
的解是 ( )




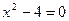 的解是( ).
的解是( ). 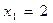 ,
,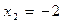
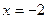
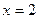
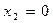
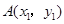 、
、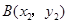 、
、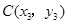 是函数
是函数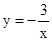 图象上的三点,且
图象上的三点,且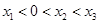 ,则
,则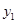 、
、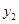 、
、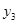 的大小关系是( )
的大小关系是( )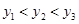
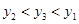
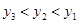
 ,则∠A=
,则∠A=  的根的判别式
的根的判别式 ____
____ 的图象经过点(3,-4
的图象经过点(3,-4 ),则此函数在每一个象限内
),则此函数在每一个象限内 随
随 的增大而
的增大而 =14cm,则阴影部分的面积_________cm2
=14cm,则阴影部分的面积_________cm2
 的边长为3,
的边长为3, 为
为 边上一点,
边上一点,  .以点
.以点 为中心,把△
为中心,把△ 顺时针旋转
顺时针旋转 ,得△
,得△ ,连接
,连接 ,则
,则


 AB、AE的数量关系,并说明理由;
AB、AE的数量关系,并说明理由; 粤公网安备 44130202000953号
粤公网安备 44130202000953号