湖北省黄冈市初二上学期期末数学卷
关于 的方程
的方程 的根的情况是( )
的根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 | C.没有实数根 | D.不能确定 |
如图,在⊙O中,弦AB、CD相交于点P,∠A=40°,∠APD=75°,则∠B=
A.15° B.35° C.40° D.75°
如图,在Rt△ABC中,∠C=90°,AC=4,BC=2,分别以AC、BC为直径画半圆,则图中阴影部分的面积为___________.(用含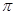 的代数式表示)
的代数式表示)
(1)探究下表中的奥秘,并完成填空:
| 一元二次方程 |
根 |
二次三项式 |
 |
 |
 |
 |
 |
 |
 |
________________ |
 |
 |
 |
 |
 |
_________________ |
 |
(2)仿照上表把二次三项式 (其中
(其中 )进行分解?
)进行分解?
在一张桌子的桌面长为6m,宽为4m,台布面积是桌面面积的2倍,如果将台布铺在桌子上,各边垂下的长度相同,求这块台布的长和宽?
如图,已知抛物线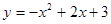 与
与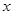 轴的两个交点为A、B,与
轴的两个交点为A、B,与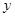 轴交于点C
轴交于点C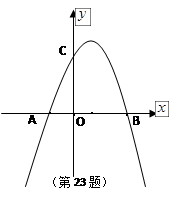
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
如图,等边三角形ABC边长为4,E是边BC上一动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB,设EC=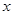 (0<
(0<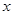 ≤2).
≤2).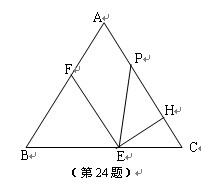
(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线)。
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求□EFPQ的面积(用含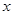 的代数式表示)?
的代数式表示)?
(3)当(2)中的平行四边形面积最大时,以E为圆心, 为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应
为半径作圆,根据⊙E与此时□EFPQ四条边交点的总个数,求相应 的取值范围
的取值范围
对称现象无处不在,请你观察下面的四个图形,它们体现了中华民族的传统文化,其中,可以看作是轴对称图形的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下面是某同学在一次作业中的计算摘录:
①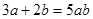 ; ②
; ② ;
;
③ ;④
;④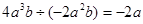 ;
;
⑤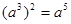 ; ⑥
; ⑥ 。
。
其中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,点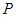 是
是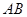 上任意一点,
上任意一点, ,还应补充一个条件,才能推出
,还应补充一个条件,才能推出 .从下列条件中补充一个条件,不一定能推出
.从下列条件中补充一个条件,不一定能推出 的是
的是
A.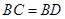 |
B.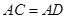 |
C.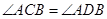 |
D.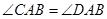 |
直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为( )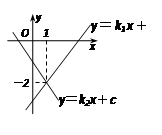
| A.x>1 | B.x<1 | C.x>-2 | D.x<-2 |
图①是一个边长为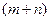 的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )
的正方形,小颖将图①中的阴影部分拼成图②的形状,由图①和图②能验证的式子是( )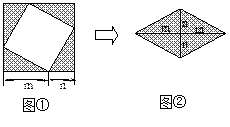
A. |
B.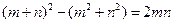 |
C.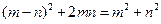 |
D. |
如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为
A、2 B、3 C、4 D、5
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为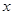 ,△ ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
,△ ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )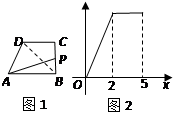
| A.3 | B.4 | C.5 | D.6 |
请你写出同时满足下列两个条件的一个一次函数的解析式:①y随x的增大而减小;②该直线可以和两坐标轴围成三角形_______
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______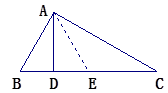
小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.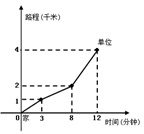
下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是_______
有一轮船由东向西航行,在A处测得西偏北15º有一灯塔P.继续航行10海里后到B处,又测得灯塔P在西偏北30º.如果轮船航向不变,则灯塔与船之间的最近距离是
如图,在直角坐标系中,△ABC是关于直线y=1成轴对称的图形,已知点A坐标是(4,4),则点B的坐标是________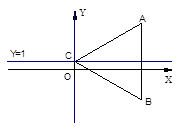
如图所示,直线y=x+1与y轴相交于点A1,以OA1为边作正方形OA1B1C1,记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2,再以C1A2为边作正方形C1A2B2C2,记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3,再以C2A3为边作正方形C2A3B3C3,记作第三个正方形;…依此类推,则第n个正方形的边长为______________
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.试判断△OEF的形状,并说明理由.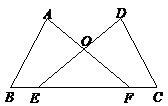
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.供选择的三个条件(请从其中选择一个):
① AB=ED; ②BC=EF; ③∠ACB=∠DFE.
如图:已知直线L的解析式为y=-3x+3,且L与x轴交于点D,直线m经过点A、B,直线L、m交于点C。
(1)、求直线m的解析式;
(2)、在直线m上存在异于点C的点P,使得△ADP与△ADC的面积相等,请求出点C的坐标
一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
⑴如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
⑵如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多可获得多少利润?此时如何分配加工时间?
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为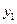 、
、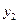 (km),
(km),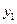 、
、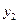 与x的函数关系如图所示.
与x的函数关系如图所示.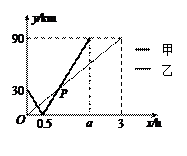
(1)填空:A、C两港口间的距离为 km,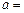 ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.

 ,则正六边形的边长为( )
,则正六边形的边长为( )




 有意义的
有意义的 的取值范围是_______
的取值范围是_______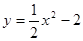 的图象上的一个点,写出一个
的图象上的一个点,写出一个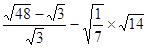
 ,其中
,其中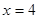
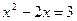


 ,BC=8,则AC等于
,BC=8,则AC等于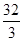
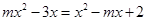 是关于
是关于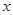 的一元二次方程,则
的一元二次方程,则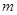 的取值范围为
的取值范围为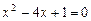 时,配方后所得的方程是
时,配方后所得的方程是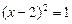

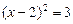
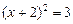
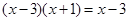 的解是
的解是 
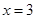

 的一元二次方程
的一元二次方程 有实根,则
有实根,则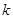 的取值范围是
的取值范围是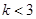
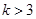
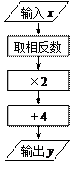
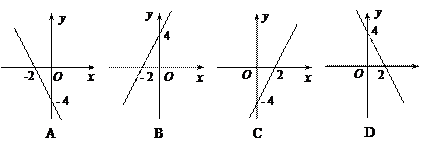
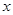 的取值范围是
的取值范围是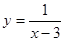
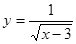

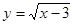

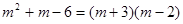

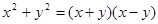
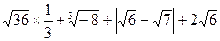 =" "
=" "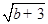 =0,则a-b的立方根是________
=0,则a-b的立方根是________
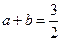 ,
,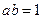 ,则
,则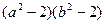 =
=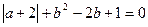 ,求代数式
,求代数式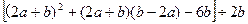 的值
的值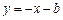 分别与x、y轴交于A
分别与x、y轴交于A 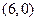 、B两点,过点B的直线交x轴负半轴于C,且
、B两点,过点B的直线交x轴负半轴于C,且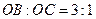 ;
; (
(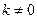 )交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得
)交AB于E,交BC于点F,交x轴于D,是否存在这样的直线EF,使得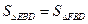 ?若存在,求出
?若存在,求出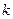 的值;若不存在,说明理由?
的值;若不存在,说明理由? 粤公网安备 44130202000953号
粤公网安备 44130202000953号