如图5,初三(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度 ,标杆与旗杆的水平距离
,标杆与旗杆的水平距离 ,人的眼睛与地面的高度
,人的眼睛与地面的高度 ,人与标杆
,人与标杆 的水平距离
的水平距离 ,求旗杆
,求旗杆 的高度.
的高度.
小明沿着坡度为1:2的山坡向上走了1000m,则他升高了 m
(结果保留根号)
图形的操作过程(本题中四个矩形的水平方向的边长均为a,竖直方向的边长均b): 
●在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);
●在图2中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图3中,请你类似地画一条有两个折点的线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1=__________,S2=__________,S3=__________.
(3)联想与探索
如上图,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草场地面积是多少?并说明你的猜想是正确的.
如图,一艘渔政船从小岛A处出发,向正北方向以每小时20海里的速度行驶了1.5小时到达B处执行任务,再向正东方向以相同的速度行驶了2小时到达C处继续执行任务,然后以相同的速度直接从C处返回A处.
(1)分别求AB、 BC的长;
(2)问返回时比出去时节省了多少时间?
如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.
(1) 用含a、b的代数式表示绿化面积;
(2) 求出当a=3米,b=2米时的绿化面积.
有一个数值转换器,原理如下图所示,当输入x的值为16时,输出y的值______.
如图(甲),在俄罗斯方块游戏中,上方小方块可先 (填“顺”或“逆”)时针旋转 度,再向 (填左或右)平移至边格,然后让它自己往下移动,最终拼成一个完整的图案如图(乙),使其自动消失.
在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,且整体图案成轴对称图形.下面是小华、小芳与小明的设计方案.
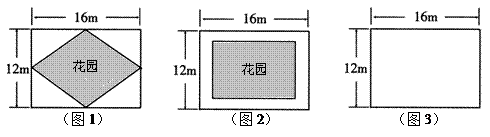
请你根据以上的对话,完成下列问题.
(1)你认为小华所设计的花园的形状是 ,整个设计图案共有 条对称轴;
(2)请你帮助小芳计算出道路的宽度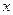 的值;
的值;
(3)请你根据小明的设计方案在图3中画出符合设计条件的草图,然后根据你所画的草图求出该等腰梯形的上底和下底的长.
某高铁工程即将动工,工程需要测量某一条河的宽度.如图,一测量员在河岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得标杆B在北偏西280处.求河宽AB.(结果精确到1米)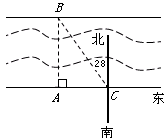
如图所示,已知:点 ,
, ,
,  .在
.在 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在 轴上,另一个顶点在
轴上,另一个顶点在 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个 ,第2个
,第2个 ,第3个
,第3个 ,…,则①
,…,则① = 度;②
= 度;② =
=
请你观察思考下列计算过程:
∵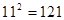 ,∴
,∴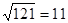 ;
;
同样:∵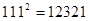 ,∴
,∴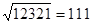 ;……………………………
;……………………………
由此猜想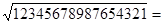 。
。
如图,小明欲利用测角仪测量树的高度.已知他离树的水平距离BC为10m,测角仪的高度CD为1.5m,测得树顶A的仰角为33°.求树的高度AB.
(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)