四川省成都市温江区初三第一学期期末数学卷
在一次初三学生数学交流会上,每两名学生握手一次,统计共握手253次。若设参加此会的学生为x名,据题意可列方程为
| A.x(x+1)=253 | B.x(x-1)=253 | C.2x(x-1)=253 | D.x(x-1)=253×2 |
已知:如图,在Rt△ABC中,∠ACB=90º,AC=6,sinB= , 点D是边BC的中点,
, 点D是边BC的中点,
CE⊥AD,垂足为E.

求:(1)线段CD的长;
(2)cos∠DCE的值.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F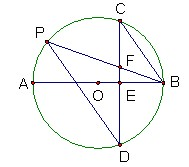
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径
(本题满分10分)
如图, 是直角三角形,
是直角三角形, ,以AB为直径的⊙O交
,以AB为直径的⊙O交 于点E,点D是BC边的中点,连结
于点E,点D是BC边的中点,连结 .
.
(1)试判断直线DE与⊙O的位置关系?并说明理由;
(2)若⊙O的半径为 ,
, ,求AE的长
,求AE的长
(本题满分10分)
某商店经销一批小家电,每个小家电的成本为40元。据市场分析,销售单价定为50元时,一个月能售出500件;若销售单价每涨1元,月销售量就减少10件.针对这种小家电的销售情况,请回答以下问题:
(1)当销售单价定为60元时,计算月销售量和月销售利润;
(2)设销售单价定为x元(x>50),月销售利润为y元,求y(用含x的代数式表示);
(3)现该商店要保证每月盈利8750元,同时又要使顾客得到实惠,那么销售单价应定为多少元?
如图,在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C. 
(1)请完成如下操作:
①以点O为原点、竖直和水平方向为轴、网格边长为单位长,建立平面直角坐标系; ②根据图形提供的信息,标出该圆弧所在圆的圆心D,
并连结AD、CD.
(2)请在(1)的基础上,完成下列填空:
①写出点的坐标:C 、D ;
②⊙D的半径= (结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的底面的面积为 ;(结果保留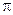 )
)
(3)若E(7,0),试判断直线EC与⊙D的位置关系,并说明你的理由
(本题满分12分)
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC,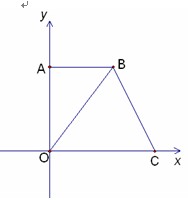
(1) 求点B的坐标;
(2) 点P从C点出发,沿线段CO以1个单位/秒的速度向终点O匀速运动,过点P作PH⊥OC,交折线C-B-O于点H,设点P的运动时间为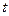 秒(
秒(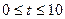 ),
),
①是否存在某个时刻,使△OPH的面积等于△OBC面积的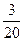 ?若存在,求出
?若存在,求出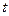
的值,若不存在,请说明理由;
②以P为圆心,PC长为半径作⊙P,当⊙P与线段OB只有一个公共点时,求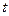 的值或
的值或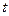 的取值范围
的取值范围
把27430按四舍五入取近似值,保留两个有效数字, 并用科学记数法表示应是( )
| A.2.8×104 | B.2.8×103 | C.2.7×104 | D.2.7×103 |
运用等式性质进行的变形,正确的是( )
| A.如果a=b,那么a+c=b-c | B.如果a2=3a,那么a=3 |
C.如果a=b,那么 |
D.如果 ,那么a=b ,那么a=b |
如图,小明将自己用的一副三角板摆成如图形状,如果∠AOB=155°,那么∠COD等于( )
| A.15° | B.25° | C.35° | D.45° |
下列说法:①锐角的补角一定是钝角;②一个角的补角一定大于这个角;③如果两个角是同一个角的余角,那么它们相等;④锐角和钝角互补.
其中,正确的说法有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下列命题中,错误的是( )
| A.矩形的对角线互相平分且相等 | B.对角线互相垂直的四边形是菱形 |
| C.等腰梯形的两条对角线相等 | D.等腰三角形底边上的中点到两腰的距离相等 |
反比例函数y= (k≠0)的图象经过点(2,5),若点(-5,n)在反比例函数的图象上,则n等于( )
(k≠0)的图象经过点(2,5),若点(-5,n)在反比例函数的图象上,则n等于( )
| A.-10 | B.-5 | C.-2 | D.-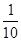 |
如图,在四边形ABCD中,E是BC边的中点,连结DE并延长交AB的延长线于F点,AB=BF。添加一个条件,使四边形ABCD是平行四边形。你认为下面四个
条件中可选择的是( )
A. |
B. |
C. |
D. |
如图所示的两个转盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是( )
(A) (B) (C) (D)
已知∠A+∠B="90°" , 且cosA = ,则cosB的值为( )
(A) (B) (C) (D)
先锋村准备在坡角为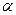 的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A.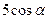 |
B.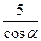 |
C.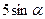 |
D.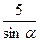 |
如图, 的直径,弦CD⊥AB于点E,且CD=3cm,⊙O的半径为
的直径,弦CD⊥AB于点E,且CD=3cm,⊙O的半径为 cm,则∠CDB的度数为( )
cm,则∠CDB的度数为( )
| A.45O | B.30O | C.90O | D.60O |
在同一时刻,两根长度不等的杆子置于阳光之下,但它们的影长相等,这两根杆子的相对位置是______________
某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为 _____m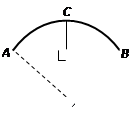
(1)计算: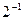 +(2π-1)0-
+(2π-1)0- sin45°-
sin45°-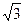 tan30°
tan30°
(2)解方程: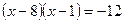
(3)一个不透明的布袋里装有4个大小、质地均相同的乒乓球,每个球上面分别标有1、2、3、4,小林先从布袋中随机抽取一个乒乓球(不放回去),再从剩下的3个球中随机抽取第二个乒乓球。
① 请你列出所有可能的结果;
② 求两次取得乒乓球的数字之积为奇数的概率。
某企业2006年盈利1500万元,2008年克服全球金融危机的不利影响,仍实现盈利2160万元。从2006年到2008年,如果该企业每年盈利的年增长率相同,求:
(1)该企业2007年盈利多少万元?
(2)若该企业盈利的年增长率继续保持不变,预计2009年盈利多少万元?
某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个。
(1)假设销售单价提高x元,那么销售300个篮球所获得的利润是____________元;这种篮球每月的销售量是___________________个。(用含x的代数式表示)
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?
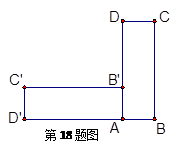
已知:如图,点A(m,3)与点B(n,2)关于直线y = x对称,且都在反比例函数 的图象上,点D的坐标为(0,-2)。
的图象上,点D的坐标为(0,-2)。
(1)求反比例函数的解析式;
(2)若过B、D的直线与x轴交于点C,求sin∠DCO的值
已知:如图,P是⊙O直径AB延长线上一点,过P的直线交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E。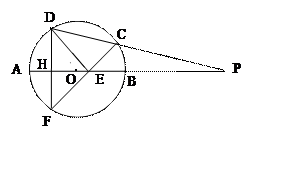
⑴ 求证:PC·PD=PO·PE;
⑵ 若DE⊥CF,∠P=150,⊙O的半径为2,求弦CF的长
如图,抛物线y=ax2+bx+c的对称轴是x=,小亮通过观察得出了下面四条信息:①c<0,②abc<0,③a-b+c>0,④2a-3b=0。你认为其中正确的有____________________。(填序号)
如图,A、B、C是⊙0上的三点,以BC为一边,作∠CBD=∠ABC,过BC上一点P,作PE∥AB交BD于点E。若∠AOC=60°,BE= ,则点P到弦AB的距离为_____
,则点P到弦AB的距离为_____
在平面直角坐标系 中,直线
中,直线 与两坐标轴围成一个△AOB。现将背面完全相同,正面分别标有数1、2、3、
与两坐标轴围成一个△AOB。现将背面完全相同,正面分别标有数1、2、3、 、
、 的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在△AOB内的概率为
的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,将该数的倒数作为点P的纵坐标,则点P落在△AOB内的概率为
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为 ,…,
,…, (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积 =_____
=_____
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、
点B的北偏东30°方向上,AB=2km,∠DAC=15°。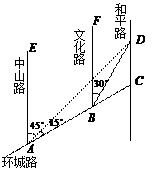
(1)求B,D之间的距离;
(2)求C,D之间的距离
如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合)。连接DP交对角线AC于E,连接BE。

(1) 证明:∠APD=∠CBE;
(2) 若∠DAB=60º,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的?
请说明理由。

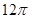


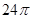
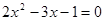 的两根为
的两根为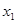 ,
,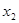 ,则
,则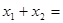 _____
_____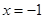 是关于
是关于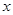 的方程
的方程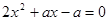 的一个根,则
的一个根,则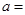 ____
____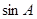 -
-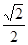 │+(
│+(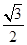 -
-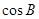 )2=0,则∠C=_______度
)2=0,则∠C=_______度 于点D,连结BD、BC,
于点D,连结BD、BC,  ,
,  ,则BD=
,则BD= 

 ,半径为2cm的
,半径为2cm的 切
切 于点
于点 ,若将
,若将 上向右滚动,则当滚动到
上向右滚动,则当滚动到 也相切时,圆心
也相切时,圆心 移动的水平距离是__________cm
移动的水平距离是__________cm


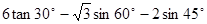


 的倒数是( )
的倒数是( )
 的系数和次数分别为( )
的系数和次数分别为( ) ,3
,3 ,3
,3






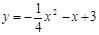 用配方法化成
用配方法化成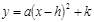 的形式( )
的形式( ) 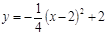
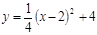
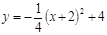
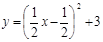
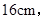 若墙上钉子间的距离
若墙上钉子间的距离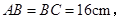 则
则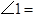 度
度
 的图象如图所示,则此抛物线的解析式为
的图象如图所示,则此抛物线的解析式为 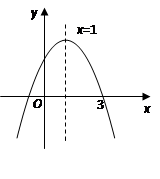
 有实数根,则实数k的取值范围是______
有实数根,则实数k的取值范围是______ 放在第二象限,斜靠在两坐标轴上,且点
放在第二象限,斜靠在两坐标轴上,且点 ,点
,点 ,如图所示:抛物线
,如图所示:抛物线 经过点
经过点 。
。
 (点
(点 仍然是以
仍然是以 为直角边的等腰直角三角形?若存在,求所有点
为直角边的等腰直角三角形?若存在,求所有点 粤公网安备 44130202000953号
粤公网安备 44130202000953号