新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 |
|
|
|
|
录播 |
4 |
16 |
12 |
8 |
直播 |
2 |
10 |
16 |
12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为 ,估计参与度在0.4以下的共有多少人?
某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
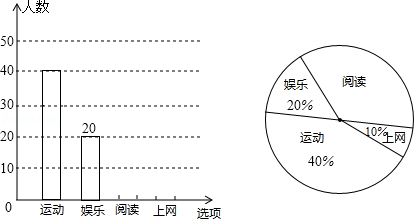
(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
甲乙两人进行射击训练,两人分别射击12次,如图分别统计了两人的射击成绩,已知甲射击成绩的方差 ,平均成绩 .
(1)根据图上信息,估计乙射击成绩不少于9环的概率是多少?
(2)求乙射击的平均成绩的方差,并据此比较甲乙的射击“水平”.
.

一只不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
| 摸球的次数 |
200 |
300 |
400 |
1000 |
1600 |
2000 |
| 摸到白球的频数 |
72 |
93 |
130 |
334 |
532 |
667 |
| 摸到白球的频率 |
0.3600 |
0.3100 |
0.3250 |
0.3340 |
0.3325 |
0.3335 |
(1)该学习小组发现,摸到白球的频率在一个常数附近摆动,这个常数是 .(精确到 ,由此估出红球有 个.
(2)现从该袋中摸出2个球,请用树状图或列表的方法列出所有等可能的结果,并求恰好摸到1个白球,1个红球的概率.
为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:,并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
(1)填空:样本容量为 , ;
(2)把频数分布直方图补充完整;
(3)若从该地随机抽取1名学生,估计这名学生身高低于的概率.

某甜品店计划订购一种鲜奶,根据以往的销售经验,当天的需求量与当天的最高气温 有关,现将去年六月份(按30天计算)的有关情况统计如下:
(最高气温与需求量统计表)
| 最高气温 (单位: |
需求量(单位:杯) |
|
|
200 |
|
|
250 |
|
|
400 |
(1)求去年六月份最高气温不低于 的天数;
(2)若以最高气温位于各区间的频率估计最高气温位于该区间的概率,求去年六月份这种鲜奶一天的需求量不超过200杯的概率;
(3)若今年六月份每天的进货量均为350杯,每杯的进价为4元,售价为8元,未售出的这种鲜奶厂家以1元的价格收回销毁,假设今年与去年的情况大致一样,若今年六月份某天的最高气温 满足 (单位: ,试估计这一天销售这种鲜奶所获得的利润为多少元?

某种机器使用若干年后即被淘汰,该机器有一易损零件,为调查该易损零件的使用情况,随机抽取了100台已被淘汰的这种机器,经统计:每台机器在使用期内更换的该易损零件数均只有8,9,10,11这四种情况,并整理了这100台机器在使用期内更换的该易损零件数,绘制成如图所示不完整的条形统计图.
(1)请补全该条形统计图;
(2)某公司计划购买一台这种机器以及若干个该易损零件,用上述100台机器更换的该易损零件数的频率代替一台机器更换的该易损零件数发生的概率.
①求这台机器在使用期内共更换了9个该易损零件的概率;
②若在购买机器的同时购买该易损零件,则每个200元;若在使用过程中,因备用该易损零件不足,再购买,则每个500元.请你帮该公司用花在该易损零件上的费用的加权平均数进行决策:购买机器的同时应购买几个该易损零件,可使公司的花费最少?

某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好,并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次研究中,一共调查了 名学生;若该校共有1500名学生,估计全校爱好运动的学生共有 名;
(2)补全条形统计图,并计算阅读部分圆心角是 ;
(3)在全校同学中随机选出一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生概率是 .
在一个不透明的盒子中,共有“一白三黑” 个围棋子,它们除了颜色之外没有其它区别.
个围棋子,它们除了颜色之外没有其它区别.
(1)随机地从盒中提出 子,则提出白子的概率是多少?
子,则提出白子的概率是多少?
(2)随机地从盒中提出 子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.
子,不放回再提第二子.请你用画树状图或列表的方法表示所有等可能的结果,并求恰好提出“一黑一白”子的概率.
在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共5只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
58 |
96 |
116 |
295 |
484 |
601 |
摸到白球的频率 |
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)试估算口袋中白种颜色的球有多少只?
(3)请画树状图或列表计算:从中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?
初三年级组织冬季拔河比赛,先用抽签的方法两两一组进行初赛,初三年级共有(1)(2)(3)(4)四个班,小明是初三(1)班的学生,他说“我们班和初三(2)班恰好分在同一组的概率是 ”你认为正确吗?如果正确,说明理由;如果不正确,写出正确的解答过程.
”你认为正确吗?如果正确,说明理由;如果不正确,写出正确的解答过程.
九年级某班同学在庆祝2015年元旦晚会上进行抽奖活动.在一个不透明的口袋中有三个完全相同的小球,把它们分别标号1、2、3.随机摸出一个小球记下标号后放回摇匀,再从中随机摸出一个小球记下标号.
(1)请用列表或画树形图的方法(只选其中一种),表示两次摸出小球上的标号的所有结果;
(2)规定当两次摸出的小球标号相同时中奖,求中奖的概率.
有四张背面图案相同的卡片A、B、C、D,其正面分别画有四个不同的几何图形(如图).小敏将这四张卡片背面朝上洗匀摸出一张,放回洗匀再摸出一张.
(1)用树状图(或列表法)表示两次摸出卡片所有可能的结果;(卡片可用A、B、C、D表示)
(2)求摸出的两张卡片图形都是中心对称图形的概率.
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.
甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、丙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率。