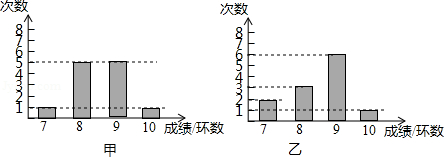
甲乙两人进行射击训练,两人分别射击12次,如图分别统计了两人的射击成绩,已知甲射击成绩的方差 ,平均成绩 .
(1)根据图上信息,估计乙射击成绩不少于9环的概率是多少?
(2)求乙射击的平均成绩的方差,并据此比较甲乙的射击“水平”.
.
推荐套卷
甲乙两人进行射击训练,两人分别射击12次,如图分别统计了两人的射击成绩,已知甲射击成绩的方差 ,平均成绩 .
(1)根据图上信息,估计乙射击成绩不少于9环的概率是多少?
(2)求乙射击的平均成绩的方差,并据此比较甲乙的射击“水平”.
.
