2021年是中国共产党建党100周年,某校开展了全校教师学习党史活动并进行了党史知识竞赛,从七、八年级中各随机抽取了20名教师,统计这部分教师的竞赛成绩(竞赛成绩均为整数,满分为10分,9分及以上为优秀).相关数据统计、整理如下:
抽取七年级教师的竞赛成绩(单位:分)
6,7,7,8,8,8,8,8,8,8,8,9,9,9,9,10,10,10,10,10.
七八年级教师竞赛成绩统计表
|
年级 |
七年级 |
八年级 |
|
平均数 |
8.5 |
8.5 |
|
中位数 |
|
9 |
|
众数 |
8 |
|
|
优秀率 |
|
|
根据以上信息,解答下列问题:
(1)填空: , ;
(2)估计该校七年级120名教师中竞赛成绩达到8分及以上的人数;
(3)根据以上数据分析,从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异.

"惜餐为荣,殄物为耻",为了解落实"光盘行动"的情况,某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量.从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据(单位: ,进行整理和分析(餐厨垃圾质量用 表示,共分为四个等级: . , , , . ,下面给出了部分信息.
七年级10个班的餐厨垃圾质量:0.8,0.8,0.8,0.9,1.1,1.1,1.6,1.7,1.9,2.3.
八年级10个班的餐厨垃圾质量中 等级包含的所有数据为:1.0,1.0,1.0,1.0,1.2.
七、八年级抽取的班级餐厨垃圾质量统计表
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
等级所占百分比 |
|
七年级 |
1.3 |
1.1 |
|
0.26 |
|
|
八年级 |
1.3 |
|
1.0 |
0.23 |
|
根据以上信息,解答下列问题:
(1)直接写出上述表中 , , 的值;
(2)该校八年级共30个班,估计八年级这一天餐厨垃圾质量符合 等级的班级数;
(3)根据以上数据,你认为该校七、八年级的"光盘行动",哪个年级落实得更好?请说明理由(写出一条理由即可).

某校将学生体质健康测试成绩分为 , , , 四个等级,依次记为4分,3分,2分,1分.为了解学生整体体质健康状况,拟抽样进行统计分析.
(1)以下是两位同学关于抽样方案的对话:
小红:"我想随机抽取七年级男、女生各60人的成绩."
小明:"我想随机抽取七、八、九年级男生各40人的成绩."
根据如图学校信息,请你简要评价小红、小明的抽样方案.
如果你来抽取120名学生的测试成绩,请给出抽样方案.
(2)现将随机抽取的测试成绩整理并绘制成如图统计图,请求出这组数据的平均数、中位数和众数.

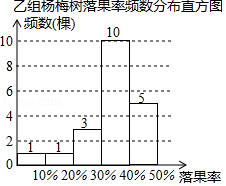
杨梅果实成熟期正值梅雨季节,雨水过量会导致杨梅树大量落果,给果农造成损失.为此,市农科所开展了用防雨布保护杨梅果实的实验研究.在某杨梅果园随机选择40棵杨梅树,其中20棵加装防雨布(甲组),另外20棵不加装防雨布(乙组).在杨梅成熟期,统计了甲、乙两组中每一棵杨梅树的落果率(落地的杨梅颗数占树上原有杨梅颗数的百分比),绘制成统计图表(数据分组包含左端值不包含右端值).
甲组杨梅树落果率频数分布表
|
落果率 |
组中值 |
频数(棵 |
|
|
|
12 |
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
1 |
(1)甲、乙两组分别有几棵杨梅树的落果率低于 ?
(2)请用落果率的中位数或平均数,评价市农科所"用防雨布保护杨梅果实"的实际效果;
(3)若该果园的杨梅树全部加装这种防雨布,落果率可降低多少?说出你的推断依据.
为了更好地了解党的历史,宣传党的知识,传颂英雄事迹,某校团支部组建了: .党史宣讲; .歌曲演唱; .校刊编撰; .诗歌创作等四个小组,团支部将各组人数情况制成了统计图表(不完整).
各组参加人数情况统计表
|
小组类别 |
|
|
|
|
|
人数(人 |
10 |
|
15 |
5 |
根据统计图表中的信息,解答下列问题:
(1)求 和 的值;
(2)求扇形统计图中 所对应的圆心角度数;
(3)若在某一周各小组平均每人参与活动的时间如下表所示:
|
小组类别 |
|
|
|
|
|
平均用时(小时) |
2.5 |
3 |
2 |
3 |
求这一周四个小组所有成员平均每人参与活动的时间.

现有甲、乙两种糖果的单价与千克数如下表所示.
|
甲种糖果 |
乙种糖果 |
|
|
单价(元 千克) |
30 |
20 |
|
千克数 |
2 |
3 |
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为 元 千克.
某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位: .根据调查结果,绘制出如下的统计图①和图②.

请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中 的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
某中学规定学生的学期体育成绩满分为100,其中体育课外活动占 ,期末考试成绩占 ,小彤的这两项成绩依次是90,80.则小彤这学期的体育成绩是 .
某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:

|
考生 |
自选项目 |
长跑 |
掷实心球 |
|
小红 |
95 |
90 |
95 |
|
小强 |
90 |
95 |
95 |
①补全条形统计图.
②如果体育中考按自选项目占 、长跑占 、掷实心球占 计算成绩(百分制),分别计算小红和小强的体育中考成绩.
某中学全校师生听取了"禁毒"宣传报告后,对禁毒人员肃然起敬.学校德育处随后决定在全校1000名学生中开展"我为禁毒献爱心"的捐款活动.张老师在周五随机调查了部分学生随身携带零花钱的情况,并将收集的数据进行整理,绘制了如图所示的条形统计图.
(1)求这组数据的平均数和众数;
(2)经调查,当学生身上的零花钱多于15元时,都愿捐出零花钱的 ,其余学生不参加捐款.请你估计周五这一天该校可能收到学生自愿捐款多少元?
(3)捐款最多的两人将和另一个学校选出的两人组成一个"禁毒"知识宣讲小组,若从4人中随机指定两人担任正、副组长,求这两人来自不同学校的概率.

今年9月,第十四届全国运动会将在陕西省举行.本届全运会主场馆在西安,开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温,从中随机抽取了60天的日平均气温,并绘制成如下统计图:

根据以上信息,回答下列问题:
(1)这60天的日平均气温的中位数为 ,众数为 ;
(2)求这60天的日平均气温的平均数;
(3)若日平均气温在 的范围内(包含 和 为"舒适温度".请预估西安市今年9月份日平均气温为"舒适温度"的天数.
为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
|
一分钟跳绳个数(个 |
141 |
144 |
145 |
146 |
|
学生人数(名 |
5 |
2 |
1 |
2 |
则关于这组数据的结论正确的是
| A. |
平均数是144 |
B. |
众数是141 |
| C. |
中位数是144.5 |
D. |
方差是5.4 |
2021年是中国共产党成立100周年.为普及党史知识,培养爱国主义精神,今年五月份,某市党校举行党史知识竞赛,每个班级各选派15名学员参加了网上测试,现对甲、乙两班学员的分数进行整理分析如下:
甲班15名学员测试成绩(满分100分)统计如下:
87,84,88,76,93,87,73,98,86,87,79,85,84,85,98.
乙班15名学员测试成绩(满分100分)统计如下:
77,88,92,85,76,90,76,91,88,81,85,88,98,86,89
(1)按如表分数段整理两班测试成绩
|
班级 |
|
|
|
|
|
|
|
甲 |
1 |
2 |
|
5 |
1 |
2 |
|
乙 |
0 |
3 |
3 |
6 |
2 |
1 |
表中 ;
(2)补全甲班15名学员测试成绩的频数分布直方图;
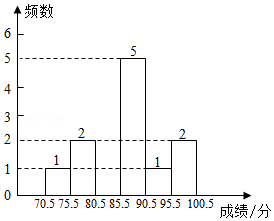
(3)两班测试成绩的平均数、众数、中位数、方差如表所示:
|
班级 |
平均数 |
众数 |
中位数 |
方差 |
|
甲 |
86 |
|
86 |
44.8 |
|
乙 |
86 |
88 |
|
36.7 |
表中 , .
(4)以上两个班级学员掌握党史相关知识的整体水平较好的是 班;
(5)本次测试两班的最高分都是98分,其中甲班2人,乙班1人.现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛,根据树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率.

实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了解梁家岭村今年一季度经济发展状况,小玉同学的课题研究小组从该村300户家庭中随机抽取了20户,收集到他们一季度家庭人均收入的数据如下(单位:万元)
0.69 0.73 0.74 0.80 0.81 0.98 0.93 0.81 0.89 0.69
0.74 0.99 0.98 0.78 0.80 0.89 0.83 0.89 0.94 0.89
研究小组的同学对以上数据进行了整理分析,得到下表:
|
分组 |
频数 |
|
|
2 |
|
|
3 |
|
|
1 |
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
统计量 |
平均数 |
中位数 |
众数 |
|
数值 |
0.84 |
|
|
(1)表格中: , , , ;
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数;
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请说明理由.