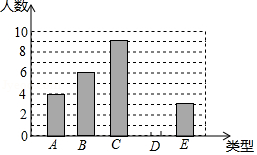
某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用 、 、 、 、 表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了八年级50名学生最近一周的读书时间,统计数据如下表:
时间(小时) |
6 |
7 |
8 |
9 |
10 |
人数 |
5 |
8 |
12 |
15 |
10 |
(1)写出这50名学生读书时间的众数、中位数、平均数;
(2)根据上述表格补全下面的条形统计图.
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于9小时的概率是多少?

某篮球队10名队员的年龄结构如表,已知该队队员年龄的中位数为21.5,则众数与方差分别为
年龄 |
19 |
20 |
21 |
22 |
24 |
26 |
人数 |
1 |
1 |
|
|
2 |
1 |
A.22,3B.22,4C.21,3D.21,4
近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,自2016年国庆后,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 |
0 |
1 |
2 |
3 |
4 |
5 |
人数 |
11 |
15 |
23 |
28 |
18 |
5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 ,该中位数的意义是 ;
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
在课外活动中,有10名同学进行了投篮比赛,限每人投10次,投中次数与人数如下表:
投中次数 |
5 |
7 |
8 |
9 |
10 |
人数 |
2 |
3 |
3 |
1 |
1 |
则这10人投中次数的平均数和中位数分别是
A.3.9,7B.6.4,7.5C.7.4,8D.7.4,7.5
某公司共有 、 、 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
各部门人数及每人所创年利润统计表
部门 |
员工人数 |
每人所创的年利润 万元 |
|
5 |
10 |
|
|
8 |
|
|
5 |
(1)①在扇形图中, 部门所对应的圆心角的度数为
②在统计表中, ,
(2)求这个公司平均每人所创年利润.

为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:
户外活动的时间(小时) |
1 |
2 |
3 |
6 |
学生人数(人 |
2 |
2 |
4 |
2 |
则关于“户外活动时间”这组数据的众数、中位数、平均数分别是
A.3、3、3B.6、2、3C.3、3、2D.3、2、3
李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) |
2 |
2.5 |
3 |
3.5 |
4 |
学生人数(名 |
1 |
2 |
8 |
6 |
3 |
则关于这20名学生阅读小时数的说法正确的是
A.众数是8B.中位数是3C.平均数是3D.方差是0.34
下表是某位男子马拉松长跑运动员近6次的比赛成绩(单位:分钟)
第几次 |
1 |
2 |
3 |
4 |
5 |
6 |
比赛成绩 |
145 |
147 |
140 |
129 |
136 |
125 |
则这组成绩的中位数和平均数分别为
A.137、138B.138、137C.138、138D.137、139
某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为100,所占比例如下表:
项目 |
学习 |
卫生 |
纪律 |
活动参与 |
所占比例 |
|
|
|
|
八年级2班这四项得分依次为80,90,84,70,则该班四项综合得分(满分 为
A.81.5B.82.5C.84D.86
某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如下表所示:
课外阅读时间(小时) |
0.5 |
1 |
1.5 |
2 |
人数 |
2 |
3 |
4 |
1 |
那么这10名学生平均每天的课外阅读时间的平均数和众数分别是
A.1.2和1.5B.1.2和4C.1.25和1.5D.1.25 和4
自新冠肺炎疫情爆发以来,我国人民上下一心,团结一致,基本控制住了疫情.然而,全球新冠肺炎疫情依然严重,境外许多国家的疫情尚在继续蔓延,疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.

根据上面图表信息,回答下列问题:
(1)截止5月31日该国新冠肺炎感染总人数累计为 万人,扇形统计图中 岁感染人数对应圆心角的度数为 ;
(2)请直接在图中补充完整该国新冠肺炎感染人数的折线统计图;
(3)在该国所有新冠肺炎感染病例中随机地抽取1人,求该患者年龄为60岁或60岁以上的概率;
(4)若该国感染病例中从低到高各年龄段的死亡率依次为 、 、 、 、 ,求该国新冠肺炎感染病例的平均死亡率.
《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格.某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了 的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示.
各等级学生平均分统计表
等级 |
优秀 |
良好 |
及格 |
不及格 |
平均分 |
92.1 |
85.0 |
69.2 |
41.3 |
(1)扇形统计图中“不及格”所占的百分比是 ;
(2)计算所抽取的学生的测试成绩的平均分;
(3)若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级.

某班为了解同学们一周在校参加体育锻炼的时间,随机调查了10名同学,得到如下数据:
锻炼时间(小时) |
5 |
6 |
7 |
8 |
人数 |
1 |
4 |
3 |
2 |
则这10名同学一周在校参加体育锻炼时间的平均数是 小时.
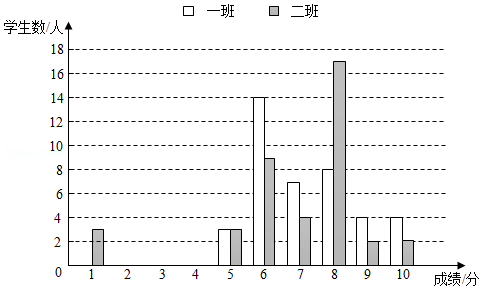
8年级某老师对一、二班学生阅读水平进行测试,并将成绩进行了统计,绘制了如下图表(得分为整数,满分为10分,成绩大于或等于6分为合格,成绩大于或等于9分为优秀).
平均分 |
方差 |
中位数 |
众数 |
合格率 |
优秀率 |
|
一班 |
7.2 |
2.11 |
7 |
6 |
|
|
二班 |
6.85 |
4.28 |
8 |
8 |
|
|
根据图表信息,回答问题:
(1)用方差推断, 班的成绩波动较大;用优秀率和合格率推断, 班的阅读水平更好些;
(2)甲同学用平均分推断,一班阅读水平更好些;乙同学用中位数或众数推断,二班阅读水平更好些.你认为谁的推断比较科学合理,更客观些.为什么?