小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.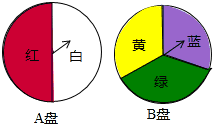
相关知识点
推荐套卷
小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.