初中数学列表法与树状图法试题

锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用（使用“求助”一次可以让主持人去掉其中一题的一个错误选项）．

（1）如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是　       　．

（2）如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是　       　．

（3）如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．

下列说法错误的是 $($ 　　 $)$

A．	必然事件发生的概率是1
B．	通过大量重复试验，可以用频率估计概率
C．	概率很小的事件不可能发生
D．	投一枚图钉，"钉尖朝上"的概率不能用列举法求得

某校组织开展运动会，小明和扎西两名同学准备从100米短跑（记为项目 $A)$，800米中长跑（记为项目 $B)$，跳远（记为项目 $C)$，跳高（记为项目 $D)$，即从 $A$， $B$， $C$， $D$四个项目中，分别选择一个项目参加比赛．请用画树状图或列表法求两名同学选到相同项目的概率．

从1、2、3、4四个数中随机选取两个不同的数，分别记为 $a$ 、 $c$ ，则关于 $x$ 的一元二次方程 $a{x}^2+4x+c=0$ 有实数解的概率为 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{1}{2}$

D．

$\frac{2}{3}$

在甲、乙两名同学中选拔一人参加“中华好诗词”大赛，在相同的测试条件下，两人5次测试成绩（单位：分）如下：

甲：79，86，82，85，83

乙：88，79，90，81，72．

回答下列问题：

（1）甲成绩的平均数是　        　，乙成绩的平均数是　      　；

（2）经计算知 $S_{甲}^2=6$， $S_{乙}^2=42$．你认为选拔谁参加比赛更合适，说明理由；

（3）如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析，求抽到的两个人的成绩都大于80分的概率．

某校为了推进学校均衡发展，计划再购进一批图书，丰富学生的课外阅读．为了解学生对课外阅读的需求情况，学校对学生所喜爱的读物： $A$．文学， $B$．艺术， $C$．科普， $D$．生活， $E$．其他，进行了随机抽样调查（规定每名学生只能选其中一类读物），并将调查结果绘制成以下不完整的统计图表．

（1） $a=$　　， $b=$　　，请补全条形统计图；

（2）如果全校有2500名学生，请你估计全校有多少名学生喜爱科普读物；

（3）学校从喜爱科普读物的学生中选拔出2名男生和3名女生，并从中随机抽取2名学生参加科普知识竞赛，请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率．

在桌面上放有四张背面完全一样的卡片，卡片的正面分别标有数字 $-1$，0，1，3．把四张卡片背面朝上，随机抽取一张，记下数字且放回洗匀，再从中随机抽取一张．则两次抽取卡片上的数字之积为负数的概率是　　．

某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等．某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是 $($ 　　 $)$

A．

$\frac{1}{5}$

B．

$\frac{1}{4}$

C．

$\frac{1}{3}$

D．

$\frac{1}{2}$

目前，全国各地正在有序推进新冠疫苗接种工作．某单位为了解职工对疫苗接种的关注度，随机抽取了部分职工进行问卷调查，调查结果分为： $A$（实时关注）、 $B$（关注较多）、 $C$（关注较少）、 $D$（不关注）四类，现将调查结果绘制成如图所示的统计图．

请根据图中信息，解答下列问题：

（1）求 $C$类职工所对应扇形的圆心角度数，并补全条形统计图；

（2）若 $D$类职工中有3名女士和2名男士，现从中任意抽取2人进行随访，请用树状图或列表法求出恰好抽到一名女士和一名男士的概率．

在中国共产党成立100周年之际，我市某中学开展党史学习教育活动．为了了解学生学习情况，在七年级随机抽取部分学生进行测试，并依据成绩（百分制）绘制出以下两幅不完整的统计图．请根据图中信息回答下列问题：

（1）本次抽取调查的学生共有 　　人，扇形统计图中表示 C等级的扇形圆心角度数为 　　．

（2） A等级中有2名男生，2名女生，从中随机抽取2人参加学校组织的知识问答竞赛，请用画树状图或列表的方法，求恰好抽到一男一女的概率．

柜子里有两双不同的鞋，如果从中随机地取出2只，那么取出的鞋是同一双的概率为 $($ 　　 $)$

A．

$\frac{1}{3}$

B．

$\frac{1}{4}$

C．

$\frac{1}{5}$

D．

$\frac{1}{6}$

某单位食堂为全体960名职工提供了 $A$， $B$， $C$， $D$四种套餐，为了解职工对这四种套餐的喜好情况，单位随机抽取240名职工进行“你最喜欢哪一种套餐（必选且只选一种）”问卷调查．根据调查结果绘制了条形统计图和扇形统计图，部分信息如下：

（1）在抽取的240人中最喜欢 $A$套餐的人数为　 　，扇形统计图中“ $C$”对应扇形的圆心角的大小为　 　 $°$；

（2）依据本次调查的结果，估计全体960名职工中最喜欢 $B$套餐的人数；

（3）现从甲、乙、丙、丁四名职工中任选两人担任“食品安全监督员”，求甲被选到的概率．

中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为 $A$， $B$， $C$， $D$四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

请你根据统计图解答下列问题：

（1）参加比赛的学生共有　　名；

（2）在扇形统计图中， $m$的值为　　，表示“ $D$等级”的扇形的圆心角为　　度；

（3）组委会决定从本次比赛获得 $A$等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知 $A$等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

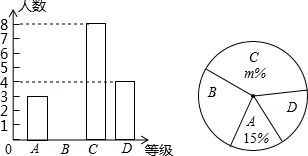
某中学以“我最喜爱的书籍”为主题，对学生最喜爱的书籍类型的情况进行了随机抽样调查（每位被调查者必须且只能选择最喜爱的一种书籍），并将调查结果绘制成如下的两幅不完整的统计图：

请根据图中提供的信息，回答下列问题：

（1）求本次被调查学生的人数；

（2）请将上面的两幅统计图补充完整；

（3）若从2名最喜爱文学书籍和2名最喜爱科普书籍的学生中随机抽取2人，请用列表或画树状图的方法求所抽取的两人恰好都是最喜爱文学书籍的概率．

随着"新冠肺炎"疫情防控形势日渐好转，各地开始复工复学，某校复学后成立"防疫志愿者服务队"，设立四个"服务监督岗"：①洗手监督岗，②戴口罩监督岗，③就餐监督岗，④操场活动监督岗．李老师和王老师报名参加了志愿者服务工作，学校将报名的志愿者随机分配到四个监督岗．

（1）李老师被分配到"洗手监督岗"的概率为 　　；

（2）用列表法或画树状图法，求李老师和王老师被分配到同一个监督岗的概率．