初中数学列表法与树状图法试题

为庆祝中国共产党成立100周年，某中学组织全校学生参加党史知识竞赛，从中任取20名学生的竞赛成绩进行统计，绘制了不完整的统计图表：

组别	成绩范围	频数
$A$	$60~70$	2
$B$	$70~80$	$m$
$C$	$80~90$	9
$D$	$90~100$	$n$

（1）分别求 $m$， $n$的值；

（2）若把每组中各学生的成绩用这组数据的中间值代替（如 $60~70$的中间值为 $65)$估计全校学生的平均成绩；

（3）从 $A$组和 $D$组的学生中随机抽取2名学生，用树状图或列表法求这2名学生都在 $D$组的概率．

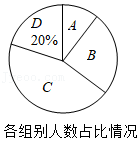
某市体育中考自选项目有乒乓球、篮球和羽毛球，每个考生任选一项作为自选考试项目．

（1）求考生小红和小强自选项目相同的概率；

（2）除自选项目之外，长跑和掷实心球为必考项目．小红和小强的体育中考各项成绩（百分制）的统计图表如下：

考生	自选项目	长跑	掷实心球
小红	95	90	95
小强	90	95	95

①补全条形统计图．

②如果体育中考按自选项目占 $50\%$、长跑占 $30\%$、掷实心球占 $20\%$计算成绩（百分制），分别计算小红和小强的体育中考成绩．

为了弘扬爱国主义精神，某校组织了"共和国成就"知识竞赛，将成绩分为： $A$ （优秀）、 $B$ （良好）、 $C$ （合格）、 $D$ （不合格）四个等级．小李随机调查了部分同学的竞赛成绩，绘制了如图统计图．

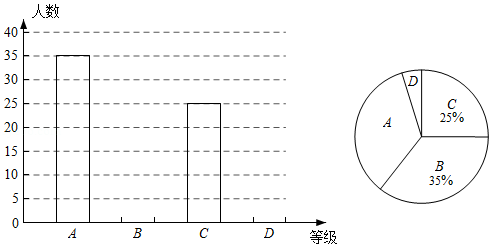
（1）本次抽样调查的样本容量是 　　，请补全条形统计图；

（2）已知调查对象中只有两位女生竞赛成绩不合格，小李准备随机回访两位竞赛成绩不合格的同学，请用树状图或列表法求出恰好回访到一男一女的概率；

（3）该校共有2000名学生，请你估计该校竞赛成绩"优秀"的学生人数．

为帮助学生养成热爱美、发现美的艺术素养，某校开展了“一人一艺”的艺术选修课活动．学生根据自己的喜好选择一门艺术项目 $(A$：书法， $B$：绘画， $C$：摄影， $D$：泥塑， $E:$剪纸），张老师随机对该校部分学生的选课情况进行调查后，制成了两幅不完整的统计图（如图所示）．

（1）张老师调查的学生人数是 　　．

（2）若该校共有学生1000名，请估计有多少名学生选修泥塑；

（3）现有4名学生，其中2人选修书法，1人选修绘画，1人选修摄影，张老师要从这4人中任选2人了解他们对艺术选修课的看法，请用画树状图或列表的方法，求所选2人都是选修书法的概率．

某中学全校师生听取了"禁毒"宣传报告后，对禁毒人员肃然起敬．学校德育处随后决定在全校1000名学生中开展"我为禁毒献爱心"的捐款活动．张老师在周五随机调查了部分学生随身携带零花钱的情况，并将收集的数据进行整理，绘制了如图所示的条形统计图．

（1）求这组数据的平均数和众数；

（2）经调查，当学生身上的零花钱多于15元时，都愿捐出零花钱的 $20\%$ ，其余学生不参加捐款．请你估计周五这一天该校可能收到学生自愿捐款多少元？

（3）捐款最多的两人将和另一个学校选出的两人组成一个"禁毒"知识宣讲小组，若从4人中随机指定两人担任正、副组长，求这两人来自不同学校的概率．

为庆祝中国共产党成立100周年，某市组织该市七、八两个年级学生参加演讲比赛，演讲比赛的主题为“追忆百年历程，凝聚青春力量”．该市一中学经过初选，在七年级选出3名同学，其中2名女生，分别记为 $x_1$、 $x_2$，1名男生，记为 $y_1$；在八年级选出3名同学，其中1名女生，记为 $x_3$，2名男生，分别记为 $y_2$、 $y_3$．现分别从两个年级初选出的同学中，每个年级随机选出一名同学组成代表队参加比赛．

（1）用列表法或树状图法（树状图也称树形图）中的一种方法，求所有可能出现的代表队总数；

（2）求选出的代表队中的两名同学恰好是一名男生和一名女生的概率 $P$．

我市于2021年5月 $22-23$日在遂宁观音湖举行了“龙舟赛”，吸引了全国各地选手参加．现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查（参与调查的同学只能选择其中一项），并将调查结果绘制出两幅不完整的统计图表，请根据统计图表回答下列问题：

类别	频数	频率
不了解	10	$m$
了解很少	16	0.32
基本了解	$b$
很了解	4	$n$
合计	$a$	1

（1）根据以上信息可知： $a=$　　， $b=$　　， $m=$　　， $n=$　　；

（2）补全条形统计图；

（3）估计该校1000名初中学生中“基本了解”的人数约有　　人；

（4）“很了解”的4名学生是三男一女，现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛，请用画树状图或列表的方法说明，抽到两名学生均为男生和抽到一男一女的概率是否相同．

看了《田忌赛马》故事后，小杨用数学模型来分析：齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为 　　．

马匹 姓名	下等马	中等马	上等马
齐王	6	8	10
田忌	5	7	9

随着手机的日益普及，学生使用手机给学校管理和学生发展带来诸多不利影响．为了保护学生视力，防止学生沉迷网络和游戏，让学生在学校专心学习，促进学生身心健康发展，教育部办公厅于2021年1月15日颁发了《教育部办公厅关于加强中小学生手机管理工作的通知》．为贯彻《通知》精神，某学校团委组织了“我与手机说再见”为主题的演讲比赛，根据参赛同学的得分情况绘制了如图所示的两幅不完整的统计图（其中 $A$表示“一等奖”， $B$表示“二等奖”， $C$表示“三等奖”， $D$表示“优秀奖” $)$．

请你根据统计图中所提供的信息解答下列问题：

（1）获奖总人数为　　人， $m=$　　；

（2）请将条形统计图补充完整；

（3）学校将从获得一等奖的4名同学（其中有一名男生，三名女生）中随机抽取两名参加全市的比赛，请根据树状图或列表法求抽取同学中恰有一名男生和一名女生的概率．

如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点 $A$ 的概率是 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{3}{8}$

D．

$\frac{4}{9}$

在桌面上放有四张背面完全一样的卡片，卡片的正面分别标有数字 $-1$，0，1，3．把四张卡片背面朝上，随机抽取一张，记下数字且放回洗匀，再从中随机抽取一张．则两次抽取卡片上的数字之积为负数的概率是　　．

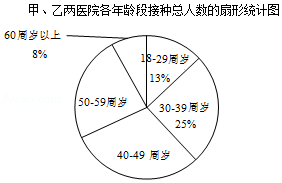
“此生无悔入华夏，来世再做中国人！”自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种“新冠”疫苗，并在全国范围内免费接种．截止2021年5月18日 $16:20$，全球接种“新冠”疫苗的比例为 $18.29\%$；中国累计接种4.2亿剂，占全国人口的 $29.32\%$．以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的扇形统计图：

	甲医院			乙医院
年龄段	频数	频率	频数		频率
$18-29$周岁	900	0.15	400		0.1
$30-39$周岁	$a$	0.25	1000		0.25
$40-49$周岁	2100	$b$	$c$		0.225
$50-59$周岁	1200	0.2	1200		0.3
60周岁以上	300	0.05	500		0.125

（1）根据上面图表信息，回答下列问题：

①填空： $a=$　　， $b=$　　， $c=$　　；

②在甲、乙两医院当天接种疫苗的所有人员中， $40-49$周岁年龄段人数在扇形统计图中所占圆心角为 　　；

（2）若 $A$、 $B$、 $C$三人都于当天随机到这两家医院接种疫苗，求这三人在同一家医院接种的概率．

某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等．某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是 $($ 　　 $)$

A．

$\frac{1}{5}$

B．

$\frac{1}{4}$

C．

$\frac{1}{3}$

D．

$\frac{1}{2}$

目前，全国各地正在有序推进新冠疫苗接种工作．某单位为了解职工对疫苗接种的关注度，随机抽取了部分职工进行问卷调查，调查结果分为： $A$（实时关注）、 $B$（关注较多）、 $C$（关注较少）、 $D$（不关注）四类，现将调查结果绘制成如图所示的统计图．

请根据图中信息，解答下列问题：

（1）求 $C$类职工所对应扇形的圆心角度数，并补全条形统计图；

（2）若 $D$类职工中有3名女士和2名男士，现从中任意抽取2人进行随访，请用树状图或列表法求出恰好抽到一名女士和一名男士的概率．

在中国共产党成立100周年之际，我市某中学开展党史学习教育活动．为了了解学生学习情况，在七年级随机抽取部分学生进行测试，并依据成绩（百分制）绘制出以下两幅不完整的统计图．请根据图中信息回答下列问题：

（1）本次抽取调查的学生共有 　　人，扇形统计图中表示 C等级的扇形圆心角度数为 　　．

（2） A等级中有2名男生，2名女生，从中随机抽取2人参加学校组织的知识问答竞赛，请用画树状图或列表的方法，求恰好抽到一男一女的概率．