如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .
(1)求证: .
(2)求 的度数.
(3)已知 ,求 的长.

在 中, 、 分别是 、 上的点,将平行四边形 沿 所在直线翻折,使点 与点 重合,且点 落在点 处.
(1)求证:△ ;
(2)连接 ,若 , ,求四边形 的面积.

如图, 与 相切于点 , 交 于点 , 的延长线交 于点 , 是 上不与 , 重合的点, .
(1)求 的大小;
(2)若 的半径为3,点 在 的延长线上,且 ,求证: 与 相切.
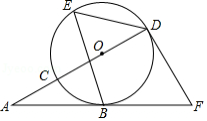
如图, 的顶点 在坐标原点, 边在 轴上, , ,把 绕点 按顺时针方向旋转到△ ,使得点 的坐标是 ,则在旋转过程中线段 扫过部分(阴影部分)的面积为 .
如图,已知 是 的直径, 是 延长线上一点, 切 于点 , 是 的弦, ,垂足为 .
(1)求证: .
(2)过点 作 交 于点 ,交 于点 ,连接 ,若 , ,求 的长.

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
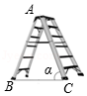
如图是一架人字梯,已知 米, 与地面 的夹角为 ,则两梯脚之间的距离 为
| A. |
米 |
B. |
米 |
C. |
米 |
D. |
米 |
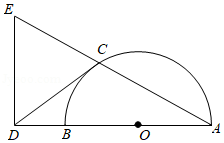
如图,已知点 是以 为直径的半圆上一点, 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,连结 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
(2)如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
(3)参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 (填推理依据),
因为 ,所以 ,
在 中, .
(填" "或" " .
所以北纬 的纬线长 .
(填相应的三角形函数值)
(结果取整数).
