如图,在 中, , , ,点 在边 上,并且 ,点 为边 上的动点,将 沿直线 翻折,点 落在点 处,则点 到边 距离的最小值是 .

如图,正方形 的对角线 上有一点 ,且 ,点 在 的延长线上,连接 ,过点 作 ,交 的延长线于点 ,连接 并延长,交 的延长线于点 ,若 , ,则线段 的长是 .

如图,平面直角坐标系中,矩形 的边 , 分别在 轴, 轴上, 点的坐标为 ,点 在矩形 的内部,点 在 边上,满足 ,当 是等腰三角形时, 点坐标为 .
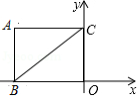
如图,边长为4的等边 , 边在 轴上,点 在 轴的正半轴上,以 为边作等边 ,边 与 交于点 ,以 为边作等边△ ,边 与 交于点 ,以 为边作等边△ ,边 与 交于点 , ,依此规律继续作等边△ ,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 , ,△ 的面积为 ,则 . ,且 为整数)

如图,在 中, ,点 是 边上的一点, 垂直平分 ,垂足为点 .若 , ,则线段 的长度为 .

如图, 是等边三角形, ,点 是边 上一点,点 是线段 上一点,连接 、 .当 , 时, .
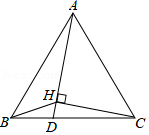
如图,矩形 中, , ,点 为 上一点,且 ,将 沿 翻折,得到△ ,连接 并延长,与 相交于点 ,则 的长为 .
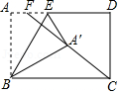
如图,一次函数 与反比例函数 的图象在第一象限交于点 ,与 轴交于点 ,与 轴交于点 ,若 ,则 .

如图,分别过 轴上的点 , , , 作 轴的垂线,与反比例函数 图象的交点分别为 , , , , 与 相交于点 , 与 相交于点 , , 与 相交于点 ,若△ 的面积记为 ,△ 的面积记为 ,△ 的面积记为 , △ 的面积记为 ,则 .

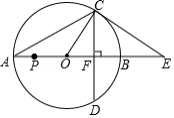
如图,以 为直径的 与 相切于点 , 交 的延长线于点 ,直径 , ,弦 ,垂足为点 ,连接 , ,则下列结论正确的是 .(写出所有正确结论的序号)
① ;
②扇形 的面积为 ;
③ ;
④若点 为线段 上一动点,则 有最大值20.25.
《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.

如图,在 中, , , , 分别为 、 、 的中点,则下列结论:① ,②四边形 为菱形,③ .其中正确的结论是 .(填写所有正确结论的序号)
