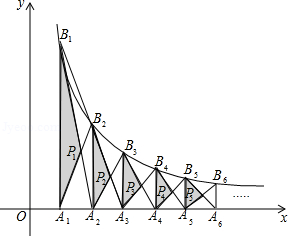
如图,分别过 轴上的点 , , , 作 轴的垂线,与反比例函数 图象的交点分别为 , , , , 与 相交于点 , 与 相交于点 , , 与 相交于点 ,若△ 的面积记为 ,△ 的面积记为 ,△ 的面积记为 , △ 的面积记为 ,则 .
推荐套卷
如图,分别过 轴上的点 , , , 作 轴的垂线,与反比例函数 图象的交点分别为 , , , , 与 相交于点 , 与 相交于点 , , 与 相交于点 ,若△ 的面积记为 ,△ 的面积记为 ,△ 的面积记为 , △ 的面积记为 ,则 .
