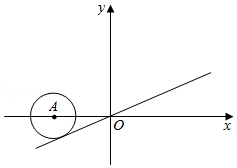
如图,直角坐标系中,以5为半径的动圆的圆心 沿 轴移动,当 与直线 只有一个公共点时,点 的坐标为
| A. |
|
B. |
|
C. |
|
D. |
|
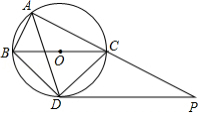
如图, 是 的外接圆,点 在 边上, 的平分线交 于点 ,连接 , ,过点 作 的切线与 的延长线交于点 .
(1)求证: ;
(2)求证: ;
(3)当 , 时,求线段 的长.
如图,在 中, ,以 的中点 为圆心, 为直径的圆交 于 , 是 的中点, 交 的延长线于 .
(1)求证: 是圆 的切线:
(2)若 , ,求 的长.

如图,在 纸片中, , , ,点 , 分别在 , 上,连结 ,将 沿 翻折,使点 的对应点 落在 的延长线上,若 平分 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
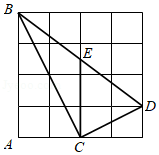
如图,在 的正方形网格中,每个小正方形的边长都为1, 为 与正方形网格线的交点,下列结论正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 直径,弦 ,垂足为点 .弦 交 于点 ,点 在 延长线上,且 .
(1)求证: 为 切线;
(2)若 , , ,求 的长.

如图,在平面直角坐标系中,矩形 ABCD的顶点 A, C分别在 x轴, y轴的正半轴上,点 , ,若反比例函数 的图象经过点 B,则 k的值为( )

| A. |
|
B. |
8 |
C. |
10 |
D. |
|
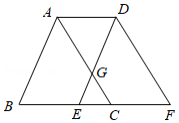
如图,将 沿 边向右平移得到 , 交 于点 .若 . .则 的值为
| A. |
2 |
B. |
4 |
C. |
6 |
D. |
8 |
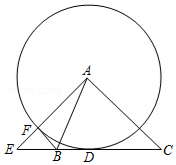
古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的圆”,请研究如下美丽的圆,如图, 中, , , ,点O在线段 上,且 ,以O为圆心. 为半径的 交线段AO于点D,交线段AO的延长线于点E.
(1)求证: 是 的切线;
(2)研究过短中,小明同学发现 ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.
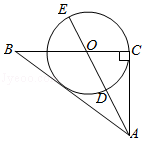
如图,点 在以 为直径的 上,点 是 的中点,连接 并延长交 于点 ,作 , 交 的延长线于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.

由四个全等的直角三角形和一个小正方形组成的大正方形 如图所示.过点 作 的垂线交小正方形对角线 的延长线于点 ,连结 ,延长 交 于点 .若 ,则 的值为
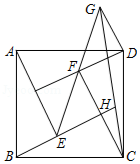
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为 的直径,弦 于点 , 于点 ,若 , ,则 的长度是
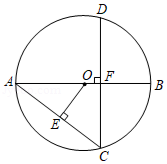
| A. |
9.6 |
B. |
|
C. |
|
D. |
10 |