初中数学相似多边形的性质解答题

如图，在平面直角坐标系中，四边形ABCD为梯形，AD∥BC，∠C=90°，tan∠ABC=2，点D（﹣8，6），将△AOB沿直线AB翻折，点O落在点E处，直线AE交x轴于点F．

（1）求点F的坐标；
（2）矩形AOCD以每秒1个单位长度的速度沿x轴向右运动，当点C′与点F重合时停止运动，运动后的矩形A′O′C′D′与△AOF重合部分的面积为S，设运动时间为t秒，求S与t的函数关系式，并直接写出自变量t的取值范围；
（3）在（2）的条件下，在矩形A′O′C′D′运动过程中，直线A′O′与射线AB交于G，是否存在时间t，使点A关于直线FG的对称点恰好落在x轴上？若存在，求t的值；若不存在，请说明理由．

如图，在Rt△ABC中，AC＝4cm，BC＝3cm，点P由B出发沿BA的方向向点A匀速运动，速度为1cm/s，同时点Q由A出发沿AC的方向向点C匀速运动，速度为2cm/s，连接PQ，设运动的时间为t（s），其中0＜t＜2，解答下列问题：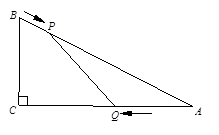

（1）当t为何值时，以P、Q、A为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，线段PQ将△ABC的面积分成1：2两部分？若存在，求出此时的t，若不存在，请说明理由；
（3）点P、Q在运动的过程中，△CPQ能否成为等腰三角形？若能，请求出此时t的值，若不存在，请说明理由．

如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

（1）求证：∠B=∠D；
（2）若AB=4，BC﹣AC=2，求CE的长．

有两个直角三角板，在三角板ABC中，∠BAC=90°，AB=AC=6，在三角板DEF中，∠FDE=90°，DF=4，DE=4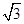，将这两个直角三角板按如图1所示位置摆放，点B与点F重合，直角边BA与FD在同一条直线上．现固定三角板ABC，将三角板DEF沿射线BA方向平行移动，当点F运动到点A时停止运动．
（1）如图2，当三角板DEF运动到点D到点A重合时，设EF与BC交于点M，则∠EMC=        度；
（2）如图3，当三角板DEF运动过程中，当EF经过点C时，求FC的长；
（3）在三角板DEF运动过程中，设BF=x，两块三角板重叠部分的面积为y，求y与x的函数解析式，并求出对应的x取值范围（直接写出结果，不必写过程）．

在平面直角坐标系中，点A的坐标为（0，1），抛物线y=ax²+bx+c的顶点为坐标原点O，且与直线y=2x-4有唯一交点B．

（1）抛物线的函数表达式为             ；
（2）如图1，设直线y=2x-4与y轴交于点D，点P是抛物线上一点．
①过点P作PE∥y轴，交直线BD于点E，若△ADE与△ABD相似，求点P的坐标；
②将△ABD沿直线BD折叠后，点A落在点C处（图2），是否存在点P，使得S_△PCD=3S△_PAB？如果存在，请求出所有满足条件的点P的坐标；如果不存在，请说明理由．

点A、B、C在同一直线上，在直线AC的同侧作△ABE和△BCF，连接AF，CE．取AF、CE的中点M、N，连接BM，BN，MN．
（1）若△ABE和△FBC是等腰直角三角形，且∠ABE=∠FBC=90°（图1），则△MBN是______三角形；
（2）在△ABE和△BCF中，若BA=BE，BC=BF，且∠ABE=∠FBC=α，（图2），则△MBN是______三角形，且∠MBN=______；
（3）若将（2）中的△ABE绕点B旋转一定角度，（图3），其他条件不变，那么（2）中的结论是否成立？若成立，给出你的证明；若不成立，写出正确的结论并给出证明．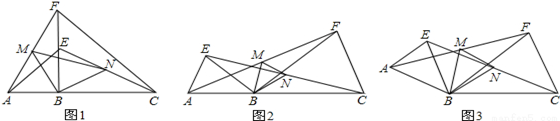

如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．

（1）求MP的值；
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）

如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．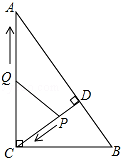

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x²+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以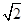个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．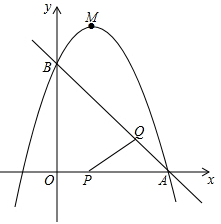

（1）求抛物线的解析式；
（2）问：当t为何值时，△APQ为直角三角形；
（3）过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标；
（4）设抛物线顶点为M，连接BP，BM，MQ，问：是否存在t的值，使以B，Q，M为顶点的三角形与以O，B，P为顶点的三角形相似？若存在，请求出t的值；若不存在，请说明理由．

如图，在Rt△ABC中，∠C＝90º，AB＝10cm，AC∶BC＝4∶3，点P从点A出发沿AB方向向点B运动，速度为1cm/s，同时点Q从点B出发沿B→C→A方向向点A运动，速度为2cm/s，当一个运动点到达终点时，另一个运动点也随之停止运动．

（1）设点P的运动时间为x（秒），△PBQ的面积为y（cm²），当△PBQ存在时，求y与x的函数关系式，并写出自变量x的取值范围；
（2）当x＝5秒时，在直线PQ上是否存在一点M，使△BCM得周长最小，若存在，求出最小周长，若不存在，请说明理由．
（3）当点Q在BC边上运动时，是否存在x，使得以△PBQ的一个顶点为圆心作圆时，另外两个顶点均在这个圆上，若存在，求出 x的值；不存在，说明理由．

如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

（1）直接写出 D，E 两点的坐标，D（         ），E（           ）
（2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？
（3）当t为何值时，DP平分∠EDA？
（4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

如图，已知在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=11，BC=13，AB=12．动点P、Q分别在边AD和BC上，且BQ=2DP．线段PQ与BD相交于点E，过点E作EF∥BC，交CD于点F，射线PF交BC的延长线于点G，设DP=x．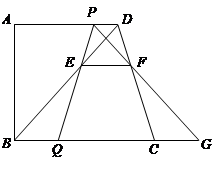

（1）求的值．
（2）当点P运动时，试探究四边形EFGQ的面积是否会发生变化？如果发生变化，请用x的代数式表示四边形EFGQ的面积S；如果不发生变化，请求出这个四边形的面积S．
（3）当△PQG是以线段PQ为腰的等腰三角形时，求x的值．

类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．
原题：如图1，在□ABCD中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若，求的值．
（1）尝试探究
在图1中，过点E作交BG于点H，则AB和EH的数量关系是          ，CG和EH的数量关系是          ，的值是         
（2）类比延伸
如图2，在原题的条件下，若（m＞0），则的值是       （用含的代数式表示），试写出解答过程．
（3）拓展迁移
如图3，梯形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F，若，（，），则的值是             （用含a、b的代数式表示）．
          

已知，如图，以点P（﹣1，0）为圆心的圆，交x轴于A、C两点（A在C的左侧），交y轴于B、D两点（B在D的上方），且∠BAC＝30°，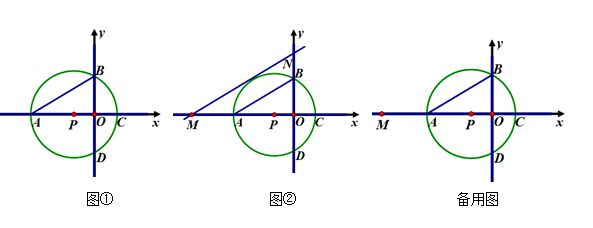

（1）如图①求⊙P的半径及点B的坐标；
（2）点Q是⊙P上任意一点，求△ABQ面积S的取值范围；
（3）如图②，已知点M（－5，0），过M作直线y=kx+b交y轴于点N，
①若MN//AB，试判断MN与⊙P的位置关系，并说明理由；
②在该直线上存在一点G，使以G、A、C为顶点的三角形是直角三角形，且满足条件的点G有且只有三个不同位置，求直线MN的函数关系式．

（本题14分）如图，在等边中，于点，点在边上运动，过点作与边交于点，连结，以为邻边作□，设□与重叠部分图形的面积为，线段的长为

（1）求线段的长（用含的代数式表示）；
（2）当四边形为菱形时，求的值；
（3）直接写出与之间的函数关系式．