初中数学相似多边形的性质解答题

正方形ABCD中，点E是CD的中点，点F在BC上，且CF：BC=1：4，你能说明AE：EF=AD：EC吗？

如图，在△中，平分交于点，交于点，，，．求与的长．

如图1，将一个直角三角板的直角顶点P放在正方形ABCD的对角线BD上滑动，并使其一条直角边始终经过点A，另一条直角边与BC相交于点E．

（1）求证：PA=PE；
（2）若将（1）中的正方形变为矩形，其余条件不变（如图2），且AD=10，DC=8，求AP：PE；
（3）在（2）的条件下，当P滑动到BD的延长线上时（如图3），请你直接写出AP：PE的比值．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求AE的长．

在Rt△ABC中，∠ACB=90°，AC=2，BC=4．点D是线段BC上的一个动点．点D与点B、C不重合，过点D作DE⊥BC交AB于点E，将△ABC沿着直线DE翻折，使点B落在直线BC上的F点．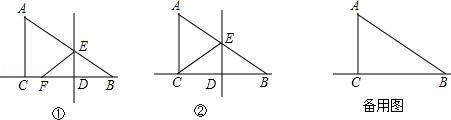

（1）设∠BAC=α（如图①），求∠AEF的大小；（用含α的代数式表示）
（2）当点F与点C重合时（如图②），求线段DE的长度；
（3）设BD=x，△EDF与△ABC重叠部分的面积为S，试求出S与x之间函数关系式，并写出自变量x的取值范围．

如图，边长为4的等边△AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长度的速度由点O向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．在点P的运动过程中，线段BP的中点为点E，将线段PE绕点P按顺时针方向旋转60°得PC．

（1）当点P运动到线段OA的中点时，点C的坐标为          ；
（2）在点P从点O到点A的运动过程中，用含t的代数式表示点C的坐标；
（3）在点P从点O到点A的运动过程中，求出点C所经过的路径长．

如图，I是△ABC的内心，∠BAC的平分线与△ABC的外接圆相交于点D，交BC于点E．

（1）求证：BD=ID；
（2）求证：ID²=DE•DA．

如图，在中，，于，若，，则为

根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．

（1）某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写"真"或"假" $)$ ．

①四条边成比例的两个凸四边形相似； $($ 　　命题）

②三个角分别相等的两个凸四边形相似； $($ 　　命题）

③两个大小不同的正方形相似． $($ 　　命题）

（2）如图1，在四边形 $\mathit{ABCD}$ 和四边形 $A_1{B}_1{C}_1{D}_1$ 中， $\angle \mathit{ABC}=\angle A_1{B}_1{C}_1$ ， $\angle \mathit{BCD}=\angle B_1{C}_1{D}_1$ ， $\frac{\mathit{AB}}{A_1{B}_1}=\frac{\mathit{BC}}{B_1{C}_1}=\frac{\mathit{CD}}{C_1{D}_1}$ ．求证：四边形 $\mathit{ABCD}$ 与四边形 $A_1{B}_1{C}_1{D}_1$ 相似．

（3）如图2，四边形 $\mathit{ABCD}$ 中， $\mathit{AB}//\mathit{CD}$ ， $\mathit{AC}$ 与 $\mathit{BD}$ 相交于点 $O$ ，过点 $O$ 作 $\mathit{EF}//\mathit{AB}$ 分别交 $\mathit{AD}$ ， $\mathit{BC}$ 于点 $E$ ， $F$ ．记四边形 $\mathit{ABFE}$ 的面积为 $S_1$ ，四边形 $\mathit{EFCD}$ 的面积为 $S_2$ ，若四边形 $\mathit{ABFE}$ 与四边形 $\mathit{EFCD}$ 相似，求 $\frac{S_2}{S_1}$ 的值．

如图，矩形PQMN内接于△ABC，矩形周长为24，AD⊥BC交PN于E，且BC＝10，AE＝16，求△ABC的面积．

如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆．小丽站在离南岸边15米的点P处看北岸，发现北岸相邻的两根电线杆A、B，恰好被南岸的两棵树C、D遮住，并且在这两棵树之间还有三棵树，求河的宽度．

如图△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，△DEA 绕点A旋转，边AD、AE与BC分别与AD、AE相交于点F、G，CB=5．
回答下列问题：

（1）求证：△GAF∽△GBA；
（2）求证：AF²=FG•FC；
（3）设y=AF²+AG²，FG=x，求y与x的函数关系式；（不要求写出自变量的取值范围）
（4）探究BF²、FG²、GC²之间的关系，证明你的结论．

如图，△ABC的边BC在直线l上，AD是△ABC的高，∠ABC=45°，BC=6cm，AB=2cm．点P从点B出发沿BC方向以1cm/s速度向点C运动，当点P到点C时，停止运动．PQ⊥BC，PQ交AB或AC于点Q，以PQ为一边向右侧作矩形PQRS，PS=2PQ．矩形PQRS与△ABC的重叠部分的面积为S（cm²），点P的运动时间为t（s）．回答下列问题：

（1）AD=         cm；
（2）当点R在边AC上时，求t的值；
（3）求S与t之间的函数关系式．

如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

（1）求证：△ADF∽△DEC；
（2）若AB=8，AD=6，AF=4，求sinB的值．

如图，矩形ABCD中，AB=6，BC=10，点P在边BC上，点Q在边CD上，

（1）如图1，将△ADQ沿AQ折叠，点D恰好与点P重合，求CQ的长；
（2）如图2，若CQ=2，且△ABP与△PCQ相似，求BP的长；
（3）若点Q是CD边上的一点，且BC上不存在满足AP⊥PQ的点P，请探究：此时CQ的长必须满足什么条件？