如图1，在△ABC中，AB＝AC，
. 过点A作BC的平行线与∠ABC的平分线交于点D，连接CD． 
（1）求证：
；
（2）点
为线段
延长线上一点，将射线GC绕着点G逆时针旋转
，与射线BD交于点E．
①若
，
，如图2所示，求证：
；
②若
，
，请直接写出
的值（用含
的代数式表示）．
为了测量路灯（OS）的高度,把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC）长为1米,然后拿竹竿向远离路灯方向走了3.2米（BB‘）,再把竹竿竖立在地面上, 测得竹竿的影长（B‘C‘）为1.8米,求路灯离地面的高度.
如图，在□ABCD中，过点B作BE⊥CD，垂足为E，连接AE．F为AE上一点，且∠BFE＝∠C．
⑴试说明：△ABF∽△EAD；
⑵若AB＝8，BE＝6，AD＝7，求BF的长．
如图，在
的正方形网格中，△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．
（1）以点O（0，0）为位似中心，按比例尺（OA︰OA’）1:3在位似中心的同侧将△OAB放大为△OA’B’，放大后点A、B的对应点分别为A’、B’ ．画出△OA’B’，并写出点A’、B’的坐标：A’（ ），B’（ ）；
（2）在（1）中，若
为线段
上任一点，写出变化后点
的对应点
的坐标（ ）．
如图，四边形ABCD是矩形，AB＝3，AD＝4，直线PS分别交AB、CD的延长线于P、S，交BC、AC、AD于Q、E、R，BP＝1，DS＝2．
（1）写出图中相似三角形（不含全等三角形）；
（2）请找出图中除AB＝CD、BC＝AD以外的相等线段，并证明你的判断．
（3）求四边形ABQR与四边形CQRD的面积比．
如本题图1，在
中，
、
、
分别为三边的中点，
点在边
上，
与四边形
的周长相等，设
、
、
.
（1）求线段
的长（用含
、
、
的代数式表示）；
（2）求证：
平分
;
（3）连接
，如本题图2，若与
相似，求证：
.
如图，在△ABC中，∠C=90°，BC=5米，AC=12米．M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒．运动时间为t秒．
（1）求线段AB的长.
（2）当t为何值时，∠AMN=∠ANM？
（3）当t为何值时，△AMN的面积最大？并求出这个最大值．
△OAB的坐标分别为O(0， 0)，A(0，4)，B(3，0)，以原点为位似中心，在第一象限将△OAB扩大，使变换得到的△OEF与△OAB对应边的比为2：1 ，
（1）画出△OEF；
（2）求四边形ABFE的面积.
如图，在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒．
（1）求直线AB的解析式；
（2）当t为何值时，△APQ与△AOB相似？
（3）当t为何值时，△APQ的面积为
个平方单位？
数学课上，李老师出示范了如下框中的题目.
小敏与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图1，确定线段AE与DB的大小关系.请你直接写出结论：AE DB（填“＞”、“＜”或“=”）；
（2）特例启发，解答题目
解：题目中，AE与DB的大小关系是：AE DB（填“＞”、“＜”或“=”）.理由如下：
如图2过点E作EF∥BC，交AC于点F；（请你完成以下解答过程）
（3）拓展结论，设计新题
在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC.若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）.
网格中每个小正方形的边长都是1.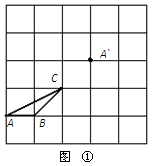
（1）将图①中的格点三角形ABC平移，使点A平移至点A`，画出平移后的三角形；
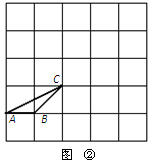
（2）在图②中画一个格点三角形DEF，使△DEF∽△ABC，且相似比为2∶1；
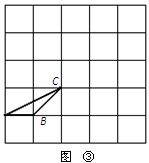
（3）在图③中画一个格点三角形PQR，使△PQR∽△ABC，且相似比为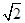
∶1.
（4）图②与图③中的△DEF与△PQR的相似比为
如图，等腰三角形ABC中，若∠A=∠B=∠DPE，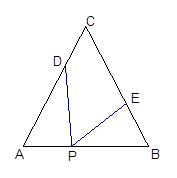
（1）求证：△APD∽△BEP;
（2）若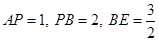
，试求出AD的长.
如图，平行四边形ABCD，DE交BC于F，交AB的延长线于E，且∠EDB=∠C.
（1）求证：△ADE∽△DBE；
（2）若DE=9cm，AE=12cm，求DC的长.
如图，△ABC在坐标平面内三个顶点的坐标分别为A（1，2）、B（3，3）、C（3，1）．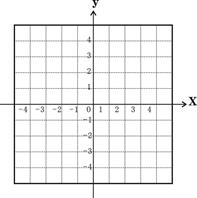
①根据题意，请你在图中画出△ABC；
②在原图中，以B为位似中心，画出△
使它与△ABC位似且相似比是3：1，并写出顶点A′和C′的坐标．
粤公网安备 44130202000953号
