如本题图1,在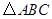 中,
中,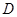 、
、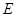 、
、 分别为三边的中点,
分别为三边的中点,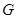 点在边
点在边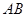 上,
上,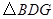 与四边形
与四边形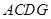 的周长相等,设
的周长相等,设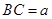 、
、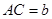 、
、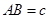 .
.
(1)求线段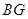 的长(用含
的长(用含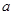 、
、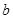 、
、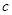 的代数式表示);
的代数式表示);
(2)求证: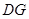 平分
平分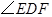 ;
;
(3)连接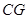 ,如本题图2,若
,如本题图2,若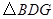 与
与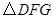 相似,求证:
相似,求证: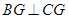 .
.
相关知识点
推荐套卷
如本题图1,在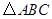 中,
中,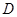 、
、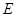 、
、 分别为三边的中点,
分别为三边的中点,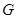 点在边
点在边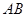 上,
上,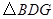 与四边形
与四边形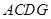 的周长相等,设
的周长相等,设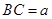 、
、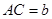 、
、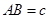 .
.
(1)求线段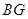 的长(用含
的长(用含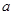 、
、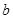 、
、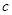 的代数式表示);
的代数式表示);
(2)求证: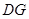 平分
平分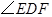 ;
;
(3)连接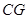 ,如本题图2,若
,如本题图2,若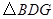 与
与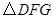 相似,求证:
相似,求证: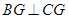 .
.