初中数学相似多边形的性质选择题

如图，在等边△ABC中，D，E，F分别是BC，AC，AB上的点，DE⊥AC，EF⊥AB，
FD⊥BC，则△DEF的面积与△ABC的面积之比等于（  ）

A．1∶3

B．2∶3

C．∶2

D．∶3

下列各组线段中,成比例的一组是(     )

A．a=	B．a=9,b=6,c=3,d=4
C．a=3,b=4,c=5,d=6	D．a=8,b=0．05,c=0．6,d=10;

如图，AB是⊙O的直径，M是⊙O上一点，MN⊥AB，垂足为N，P、Q分别是弧AM、弧BM上一点（不与端点重合）．若∠MNP=∠MNQ，下面结论：
①∠PNA=∠QNB；②∠P+∠Q=180°；③∠Q=∠PMN；④PM=QM；⑤MN2=PN•QN．
正确的结论有（ ）

A．2个

B．3个

C．4个

D．5个

如图，已知BO是△ABC的外接圆的半径，CD⊥AB于D．若AD＝3，BD＝8，CD＝6，则BO的长为 （　 　）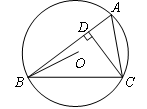

A．6               B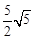．          C．          D．

若x：y=2：3，则下列各式不正确的是（ ）

A．3x=2y

B．

C．

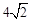D．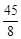

如图，在平面直角坐标系中，以原点O为位似中心，将△ABO扩大到原来的2倍，得到对应的△A′B′O．若点B的坐标是（-2，1），则点B′的坐标是（ ）

A．（4，-2）

B．（-4，2）

C．（2，-4）

D．（-2，4）

如图，△AOB以O为位似中心，扩大到△COD，各点坐标分别为：A（1，2）、B（3，0），D（4，0），则点C的坐标为（   ）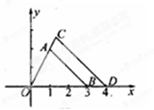

A．（2，4）

B．（，）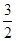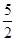

C．（，）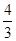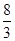

D．（，）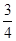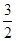

如图，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③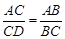； ④AC²=AD·AB．其中能够单独判定△ABC∽△ACD的条件个数为 （   ）

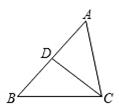
A．1          B．2       C．3        D．4

如图，为了测量一池塘的宽DE，在岸边找一点C，测得CD=30m，在DC的延长线上找一点A，测得AC=5m，过点A作AB∥DE，交EC的延长线于B，测得AB=6m，则池塘的宽DE为（   ）

A．25m

B．30m

C．36m

D．40m

如图，若P为△ABC的边AB上一点（AB＞AC），则下列条件不一定能保证△ACP∽△ABC的有（   ）

A．∠ACP=∠B     B．∠APC=∠ACB    C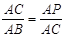．      D．

如图，DE是ΔABC的中位线，则ΔADE与ΔABC的面积之比是（   ）

A．1：1

B．1：2

C．1：3

D．1：4

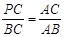
如图，在正△ABC中，D、E分别在AC、AB上，且，AE＝BE，则有（ ）

A．△AED∽△ABC      B．△ADB∽△BED  
C．△BCD∽△ABC      D．△AED∽△CBD

如图，在△ABC中，以BC为直径的圆分别交边AC、AB于D、E两点，连接BD、DE．若BD平分∠ABC，则下列结论不一定成立的是(     )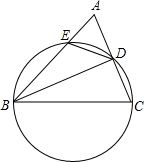

A．BD⊥AC   B．AC²=2AB·AE
C．BC＝2AD   D．△ADE是等腰三角形

已知那么下列等式中成立的是

A．

B．

C．

D．

如图，在ΔABC中，AB=30，BC=24，CA=27，  AE=EF=FB，EG∥FD∥BC，FM∥EN∥AC，则图中阴影部分的三个三角形的周长之和为（    ）

A．70

B．75

C．81

D．80