湖北省丹江口市九年级下学期第一次诊断考试数学试卷
如图,AB∥CD,点E在BC上,DE⊥BC,∠B=40°,则∠D的度数为( )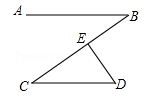
| A.40° | B.50° | C.38° | D.60° |
如图,△AOB以O为位似中心,扩大到△COD,各点坐标分别为:A(1,2)、B(3,0),D(4,0),则点C的坐标为( )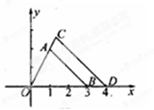
| A.(2,4) | B.(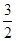 , ,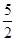 ) ) |
C.(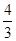 , ,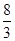 ) ) |
D.(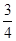 , ,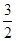 ) ) |
如图,是一个圆柱和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的主视图是( )
A.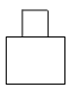 |
B.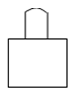 |
C.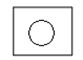 |
D.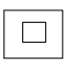 |
我市某一周的最低气温统计如下表:则这组数据的众数、中位数和平均数分别是( )
| A.2,4.5,4 | B.2,3,4 | C.2,5,3 | D.2,4,4 |
观察下列图形的构成规律,按此规律,第20个图形中棋子的个数是( )
| A.114 | B.214 | C.424 | D.444 |
如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A. |
B. |
C. |
D. |
如图,在 中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=
中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF= ∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
∠BCD,(2)EF=CF;(3)SΔBEC=2SΔCEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
小刚上网查得H N
N 禽流感病毒的直径大约是0.00000008米,将数0.00000008用科学记数法表示为 .
禽流感病毒的直径大约是0.00000008米,将数0.00000008用科学记数法表示为 .
如图,过正方形ABCD的顶点B作直线L,过A,C,D作L的垂线.垂足分别为点E,F,G.若AE=2,CF=6,则CF+AE+DG的值为 .
如图,一幢大楼的顶部竖有一块写有“校训”的宣传牌CD.小明在山坡的底部A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB垂直于视线AD,AB=20米,AE=30米,则这块宣传牌CD的高度为_ _.(测角器的高度忽略不计,结果精确到0.1米.参考数据: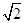 ≈1.414,
≈1.414, ≈1.732).
≈1.732).
如图,抛物线 与
与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值, 的值总是正数;②
的值总是正数;② ;③当x=0时,
;③当x=0时, ;④AB+AC=10;⑤
;④AB+AC=10;⑤ ,其中正确结论的个数是: .
,其中正确结论的个数是: .
(本小题满分6分)如图,点B在线段AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:EC=ED.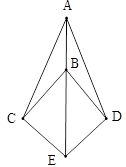
(本小题满分6分)某车间要生产220件产品,做完100件后改进了操作方法,每天多加工10件,最后总共用4天完成了任务.求改进操作方法后,每天生产多少件产品?
(本小题满分9分)某校自实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,将调查结果分成四类:A—特别好、B—好、C—一般、D—较差,并将调查结果绘制成两幅不完整的统计图.请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调查了 名同学;
(2)将条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表或画树状图的方法列出所有等可能的结果,并求出所选两位同学恰好是一位男同学和一位女同学的概率.
(本小题满分7分)已知关于x的方程 .
.
(1)当m取何值时,方程有两个实数根?
(2)设 、
、 是方程的两根,且
是方程的两根,且 ,求m的值.
,求m的值.
(本小题满分7分)已知某企业2014年用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(1)求2014年水费y(元)关于x(吨)的函数关系式;
(2)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2015年1月开始对月用水量超过96吨的企业加收污水处理费,规定:若企业月用水量x超过96吨,则除按2014年收费标准收取水费外,超过96吨部分每吨另加收 元.这样企业每月“用水费用”就可能包括水费和污水处理费.求2015年水费y(元)关于x(吨)的函数关系式.
元.这样企业每月“用水费用”就可能包括水费和污水处理费.求2015年水费y(元)关于x(吨)的函数关系式.
(本小题满分9分)如图,已知双曲线 ,双曲线
,双曲线 经过M点,且
经过M点,且 .
.
(1)求双曲线 与
与 的解析式;
的解析式;
(2)若平行于 轴的直线
轴的直线 交双曲线
交双曲线 于点A,交双曲线
于点A,交双曲线 于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
(本小题满分10分)如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
(1)求证:PD是⊙O的切线;
(2)若BD=BP= ,求图中曲边三角形(阴影部分)的周长;
,求图中曲边三角形(阴影部分)的周长;
(3)如图2,点M是 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A= ,求
,求 的值.
的值.
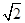 的相反数是( )
的相反数是( )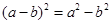
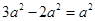
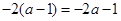
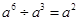
 ,则
,则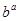 的值为( )
的值为( )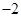
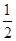
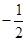
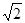 |-
|- +(π-1)
+(π-1) = .
= . 的解集为 .
的解集为 . .
. 经过点A(-3,0),B(1,0)和点C(0,-3).
经过点A(-3,0),B(1,0)和点C(0,-3). ,求点N的坐标;
,求点N的坐标;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号