(本小题满分10分)如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.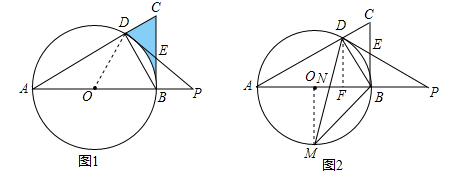
(1)求证:PD是⊙O的切线;
(2)若BD=BP=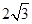 ,求图中曲边三角形(阴影部分)的周长;
,求图中曲边三角形(阴影部分)的周长;
(3)如图2,点M是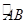 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A=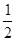 ,求
,求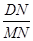 的值.
的值.
推荐套卷
(本小题满分10分)如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
(1)求证:PD是⊙O的切线;
(2)若BD=BP=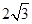 ,求图中曲边三角形(阴影部分)的周长;
,求图中曲边三角形(阴影部分)的周长;
(3)如图2,点M是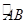 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A=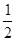 ,求
,求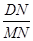 的值.
的值.