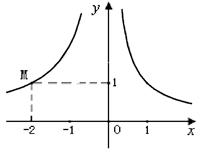
(本小题满分9分)如图,已知双曲线 ,双曲线
,双曲线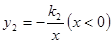 经过M点,且
经过M点,且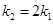 .
.
(1)求双曲线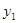 与
与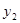 的解析式;
的解析式;
(2)若平行于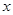 轴的直线
轴的直线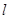 交双曲线
交双曲线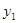 于点A,交双曲线
于点A,交双曲线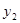 于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
相关知识点
推荐套卷
(本小题满分9分)如图,已知双曲线 ,双曲线
,双曲线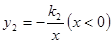 经过M点,且
经过M点,且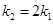 .
.
(1)求双曲线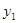 与
与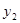 的解析式;
的解析式;
(2)若平行于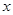 轴的直线
轴的直线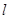 交双曲线
交双曲线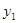 于点A,交双曲线
于点A,交双曲线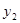 于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.
于点B,在x轴上存在两点C、D(C点在D点的左侧),使以点A、B、C、D为顶点的四边形是矩形,周长等于8,求点C,D的坐标.