如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得的仰角为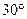 ,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为
,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为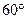 ,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)
,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)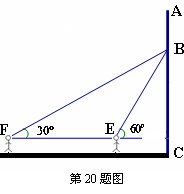
相关知识点
推荐套卷
如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得的仰角为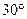 ,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为
,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为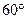 ,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)
,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)