[江苏]2014届江苏省无锡市崇安区九年级上学期期中考试数学试卷
若式子 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
| A.x≥3 | B.x≤3 | C.x>3 | D.x<3 |
矩形具有而菱形不一定具有的性质是 ( )
| A.两组对边分别平行 | B.对角线相等 |
| C.对角线互相平分 | D.两组对角分别相等 |
下列说法中,不正确的是( )
| A.过圆心的弦是圆的直径 | B.等弧的长度一定相等 |
| C.周长相等的两个圆是等圆 | D.同一条弦所对的两条弧一定是等弧 |
一元二次方程2x2-5x+1=0的根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.没有实数根 | D.无法确定 |
如图,DC是⊙O的直径,弦AB⊥CD于F,连结BC、DB,则下列结论错误的是( )

A. B.AF=BF C.OF=CF D.∠DBC=90º
B.AF=BF C.OF=CF D.∠DBC=90º
如图,点O是△ABC的内切圆的圆心,若∠A=80°,则∠BOC为( )
| A.130° | B.100° | C.50° | D.65° |
如图,已知BO是△ABC的外接圆的半径,CD⊥AB于D.若AD=3,BD=8,CD=6,则BO的长为 ( )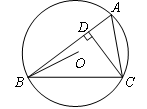
A.6 B.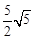 C.
C.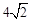 D.
D.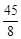
如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,ÐA=120°,则EF= cm.

如图,平面直角坐标系的长度单位是厘米,直线 分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t= 秒.
分别与x轴、y轴相交于B、A两点.点C在射线BA上以3厘米/秒的速度运动,以C点为圆心作半径为1厘米的⊙C.点P以2厘米/秒的速度在线段OA上来回运动,过点P作直线l∥x轴.若点C与点P同时从点B、点O开始运动,设运动时间为t秒,则在整个运动过程中直线l与⊙C最后一次相切时t= 秒.
如图,在四边形ABCD中,AB=BC,对角线BD平分ÐABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N.

(1)求证:ÐADB=ÐCDB;
(2)若ÐADC=90°,求证:四边形MPND是正方形.
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
| |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
| 甲 |
10 |
8 |
9 |
8 |
10 |
9 |
| 乙 |
10 |
7 |
10 |
10 |
9 |
8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2= [(x1-
[(x1- )2+(x2-
)2+(x2- )2++(xn-
)2++(xn- )2]
)2]
已知 ABCD的两边AB、AD的长是关于x的方程
ABCD的两边AB、AD的长是关于x的方程 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的边长为2,那么 ABCD的周长是多少?
ABCD的周长是多少?
把球放在长方体纸盒内,球的一部分露出盒外,如下所示为正视图.已知EF=CD=16厘米,求出这个球的半径.
如图,AB是⊙O的直径,AB=4,过点B作⊙O的切线,C是切线上一点,且BC=2,P是线段OA上一动点,连结PC交⊙O于点D,过点P作PC的垂线,交切线BC于点E,交⊙O于点F,连结DF交AB于点G.

(1)当P是OA的中点时,求PE的长;
(2)若∠PDF=∠E,求△PDF的面积.




 时,配方后所得的方程为( )
时,配方后所得的方程为( )








 ,则
,则 = .
= .

 ,且一元二次方程
,且一元二次方程 有实数根,则k的取值范围是 .
有实数根,则k的取值范围是 . ②
② ③
③
 ②
②
 ④
④ (a为常数)
(a为常数) ,0),直线
,0),直线 与x轴交于点F,与y轴交于点B,直线l∥AB且交y轴于点C,交x轴于点D,点A关于直线l的对称点为A′,连接AA′、A′D.直线l从AB出发,以每秒1个单位的速度沿y轴正方向向上平移,设移动时间为t.
与x轴交于点F,与y轴交于点B,直线l∥AB且交y轴于点C,交x轴于点D,点A关于直线l的对称点为A′,连接AA′、A′D.直线l从AB出发,以每秒1个单位的速度沿y轴正方向向上平移,设移动时间为t.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号