如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
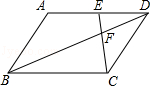
在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则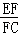 等于( )
等于( )
A.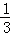 |
B.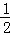 |
C. |
D. |
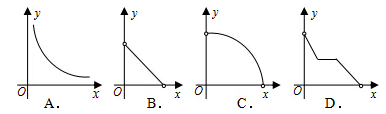
如图,△ABC中,AB=AC=2,∠BAC=20°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可表示为( )

如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
(1)求证:△ABD∽△DCE;
(2)若AB=9cm,BD=3cm,求EC的长.
若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'的度数为 ( )
| A.30° | B.50° | C.40° | D.70° |
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,且 ,
, ,求AB的值.
,求AB的值.
如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
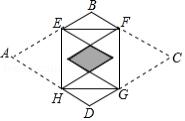
A. B.2C. D.4
如果把两条直角边长分别为5,10的直角三角形按相似比 进行缩小,得到的直角三角形的面积是 .
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
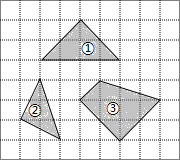
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作▱DEFA.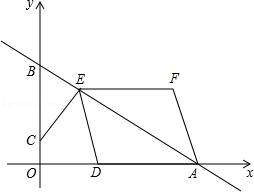
(1)当m=1时,求AE的长.
(2)当0<m<3时,若▱DEFA为矩形,求m的值;
(3)是否存在m的值,使得▱DEFA为菱形?若存在,直接写出m的值;若不存在,请说明理由.
如图,在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积比为 .

如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.