如图,矩形 的四个顶点分别在菱形 的四条边上, .将 , 分别沿边 , 折叠,当重叠部分为菱形且面积是菱形 面积的 时,则 为
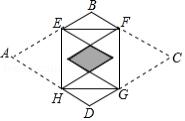
A. B.2C. D.4
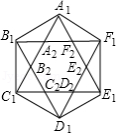
如图,正六边形 的边长为1,它的六条对角线又围成一个正六边形 ,如此继续下去,则正六边形 的面积是 .
如果把两条直角边长分别为5,10的直角三角形按相似比 进行缩小,得到的直角三角形的面积是 .
根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写"真"或"假" .
①四条边成比例的两个凸四边形相似; 命题)
②三个角分别相等的两个凸四边形相似; 命题)
③两个大小不同的正方形相似. 命题)
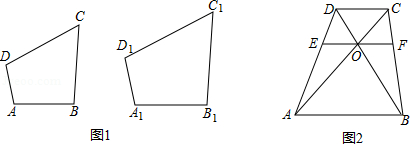
(2)如图1,在四边形 和四边形 中, , , .求证:四边形 与四边形 相似.
(3)如图2,四边形 中, , 与 相交于点 ,过点 作 分别交 , 于点 , .记四边形 的面积为 ,四边形 的面积为 ,若四边形 与四边形 相似,求 的值.
制作一块 长方形广告牌的成本是120元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的3倍,那么扩大后长方形广告牌的成本是
| A. |
360元 |
B. |
720元 |
C. |
1080元 |
D. |
2160元 |
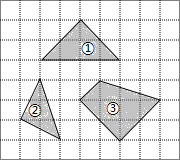
如图,在正方形网格中,每个小正方形的边长均相等.网格中三个多边形(分别标记为①,②,③ 的顶点均在格点上.被一个多边形覆盖的网格线中,竖直部分线段长度之和记为 ,水平部分线段长度之和记为 ,则这三个多边形中满足 的是
| A. |
只有② |
B. |
只有③ |
C. |
②③ |
D. |
①②③ |
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C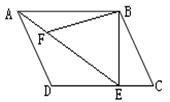
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长;
(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F, .
.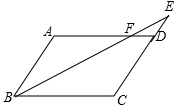
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积.
下列命题中,是真命题的为( )
| A.锐角三角形都相似 | B.直角三角形都相似 |
| C.等腰三角形都相似 | D.等边三角形都相似 |