如图,在△ABC中,D、E分别是AB、AC的中点,则△ADE与△ABC的面积比为 .

两个相似三角形的对应边分别是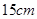 和
和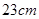 ,它们的周长相差
,它们的周长相差 ,则这两个三角形的周长分别是( )
,则这两个三角形的周长分别是( )
A. , , |
B.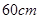 , ,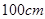 |
C.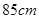 , ,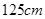 |
D.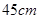 , ,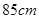 |
如图△ABC与△DEA是两个全等的等腰直角三角形,∠BAC=∠D=90°,△DEA 绕点A旋转,边AD、AE与BC分别与AD、AE相交于点F、G,CB=5.
回答下列问题:
(1)求证:△GAF∽△GBA;
(2)求证:AF2=FG•FC;
(3)设y=AF2+AG2,FG=x,求y与x的函数关系式;(不要求写出自变量的取值范围)
(4)探究BF2、FG2、GC2之间的关系,证明你的结论.
在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③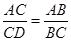 ;④AC2=AD•AB,其中单独能够判定△ABC∽△ACD的有 .
;④AC2=AD•AB,其中单独能够判定△ABC∽△ACD的有 .
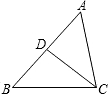
如图已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3,下列命题:
①△AED∽△BEC
②∠AEB=90°
③∠BDA=45°
④图中全等的三角形共有3对.
其中正确的命题有( )个.

| A.1 | B.2 | C.3 | D.4 |
如图,小明从路灯下A处,向前走了5米到达D处,行走过程中,他的影子将会(只填序号) .①越来越长,②越来越短,③长度不变.在D处发现自己在地面上的影子长DE是2米,如果小明的身高为1.7米,那么路灯离地面的高度AB是 米.

一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
如图,在正方形ABCD中,E、F分别是边AD、CD上的点, ,连接EF并延长交BC的延长线于点G.
,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为 ,则下列结论中正确的是( )
,则下列结论中正确的是( )

| A.m=5 | B.m=4 |
C.m=3 |
D.m=10 |
如图,已知△ABC中,点D在AC上且∠ABD=∠C,求证:AB2=AD•AC.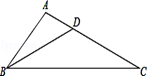
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形的面积.