一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．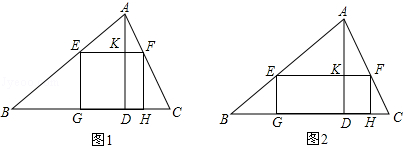
（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？
是方程组
的解，试求
的值。
的方程
和
的解相同，求
的值。
相关知识点
推荐套卷
一块材料的形状是锐角三角形ABC，边BC=120mm，高AD=80mm，把它加工成正方形零件如图1，使正方形的一边在BC上，其余两个顶点分别在AB，AC上．
（1）求证：△AEF∽△ABC；
（2）求这个正方形零件的边长；
（3）如果把它加工成矩形零件如图2，问这个矩形的最大面积是多少？
粤公网安备 44130202000953号