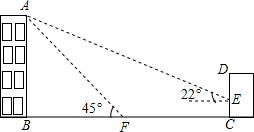
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影
子F与墙角C有13m的距离(B、F、C在一条直线上).
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22º≈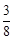 ,cos22º≈
,cos22º≈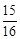 ,tan22º≈
,tan22º≈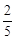 )
)
相关知识点
推荐套卷
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,
教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影
子F与墙角C有13m的距离(B、F、C在一条直线上).
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22º≈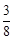 ,cos22º≈
,cos22º≈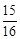 ,tan22º≈
,tan22º≈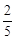 )
)