如图1,直线y=k1x与反比例函数y= (k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=
(k≠0)的图象交于点A,B,直线y=k2x与反比例函数y= 的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
(1)四边形ADBC的形状是 ;
(2)如图2,若点A的坐标为(2,4),四边形AEHC是正方形,则k2= ;
(3)如图3,若四边形EFGH为正方形,点A的坐标为(2,6),求点C的坐标;
(4)判断:随着k1、k2取值的变化,四边形ADBC能否为正方形?若能,求点A的坐标;若不能,请简要说明理由.
已知反比例函数y= (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3,求m的值.
如图,一次函数 的图象与反比例函数
的图象与反比例函数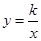 (
( )在第一象限的图象交于A(1,n)和B两点.
)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式;
(2)在第一象限内,当一次函数 的值大于反比例函数
的值大于反比例函数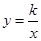 (
( )的值时,写出自变量x的取值范围.
)的值时,写出自变量x的取值范围.
如图,在平面直角坐标系xOy中,一次函数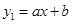 (a,b为常数,且
(a,b为常数,且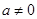 )与反比例函数
)与反比例函数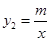 (m为常数,且
(m为常数,且 )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).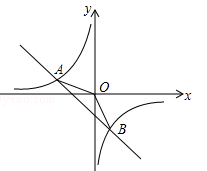
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当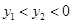 时,自变量x的取值范围.
时,自变量x的取值范围.
(本小题7分)如图,反比例函数 的图象经过点A(
的图象经过点A( ,1),射线AB与反比例函数图象交与另一点B(1,
,1),射线AB与反比例函数图象交与另一点B(1, ),射线AC与
),射线AC与 轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
(1)求 的值;
的值;
(2)求tan∠DAC的值及直线AC的解析式.
(本小题满分8分)如图所示,在平面直角坐标系xOy中,一次函数 的图象与反比例函数
的图象与反比例函数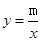 的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=
的图象交于一、三象限内的A、B两点,直线AB与x轴交于点C,点B的坐标为(-6,n),线段OA=5,E为x轴正半轴上一点,且tan∠AOE=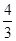 ,求△AOB的面积.
,求△AOB的面积.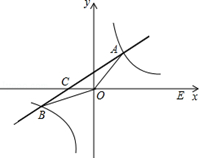
如图,已知点A(4,0),B(0, ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数 (
( )的解析式;
)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).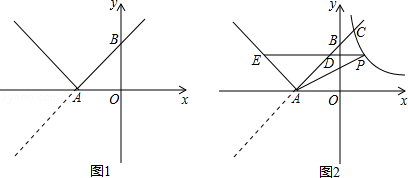
(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=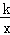 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
(本题10分)已知反比例函数 的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
(1)求反比例函数的函数解析式;
(2)当四边形OADM的面积为2时,请判断BM与DM是否相等,并说明理由.
如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y= 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
如图,在平面直角坐标系xoy中,一次函数 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.
的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.
(1)求反比例函数 的解析式;
的解析式;
(2)求点B的坐标。
一辆客车从甲地出发前往乙地,平均速度 (千米/小时)与所用时间
(千米/小时)与所用时间 (小时)的函数关系如图所示,其中
(小时)的函数关系如图所示,其中 .
.
(1)直接写出 与
与 的函数关系式;
的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶 千米,
千米, 小时后两车相遇.
小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站 、
、 ,它们相距
,它们相距 千米,当客车进入
千米,当客车进入 加油站时,货车恰好进入
加油站时,货车恰好进入 加油站(两车加油的时间忽略不计),求甲地与
加油站(两车加油的时间忽略不计),求甲地与 加油站的距离.
加油站的距离.
如图,已知一次函数 与反比例函数
与反比例函数 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 的图象,当
的图象,当 时,请直接写出自变量x的取值范围.
时,请直接写出自变量x的取值范围.
如图,直线y=x+b与双曲线y= 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
如图,已知直线y=x+k和双曲线y= (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn= ,求n的值.
,求n的值.