初中数学平行线分线段成比例解答题

如图，四边形ABCD为正方形，点A的坐标为（0，1），点B的坐标为（0，﹣2），反比例函数的图象经过点C，一次函数的图象经过A、C两点．

（1）求反比例函数与一次函数的解析式；
（2）求反比例函数与一次函数的另一个交点M的坐标；
（3）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．

如图，已知反比例函数y=的图象经过点A（-3，-2）．

（1）求反比例函数的解析式；
（2）若点B（1，m），C（3，n）在该函数的图象上，试比较m与n的大小．

如图，一次函数的图象与反比例函数的图象交于A（﹣1，m）、B（n，﹣1）两点．

（1）求一次函数的解析式；
（2）求△AOB的面积．

如图，一次函数 $y=kx+b(k<0)$的图象经过点 $C\left(3,0\right)$，且与两坐标轴围成的三角形的面积为3．

（1）求该一次函数的解析式；
（2）若反比例函数 $y=\frac{m}{x}$的图象与该一次函数的图象交于二、四象限内的 $A$、 $B$两点，且 $AC=2BC$，求 $m$的值．

一次函数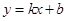与反比例函数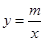的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点D．

（1）求一次函数与反比例函数的表达式；
（2）过点B作BC⊥y轴，垂足为C，连接AC交x轴于点E，求△AED的面积S．

如图，已知点A（1，2）是正比例函数y₁=kx（k≠0）与反比例函数y₂=（m≠0）的一个交点．

（1）求正比例函数及反比例函数的表达式；
（2）根据图象直接回答：在第一象限内，当x取何值时，y₁＜y₂？

如图，已知反比例函数与一次函数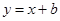的图象在第一象限相交于点A（1，﹣k+4）．

（1）试确定这两个函数的表达式；
（2）求出这两个函数图象的另一个交点B的坐标，并求△AOB的面积．

如图，反比例函数的图象与一次函数的图象交于M（1，3），N两点，点N的横坐标为﹣3．

（1）根据图象信息可得关于x的方程的解为           ；
（2）求一次函数的解析式．

如图1，已知：正比例函数y=k₁x的图象与反比例函数y=的图象交于点A（3，2）B（m，n）．我们可以发现：反比例函数的图象是一个关于原点中心对称的图形．你可以利用这一结论解决问题．
（1）填空：k₁=，a=     ，m=      ，n=        ；
（2）利用所给函数图象，写出不等式k₁x＜的解集：                ；
（3）如图2，正比例函数y=k₂x（k₂≠k₁）的图象与反比例函数y=的图象交于点P、Q，以A、B、P、Q为顶点的四边形记为代号“图形※”．
①试说明：图形※一定是平行四边形，但不可能是正方形；
②如图3，当P点在A点的左上方时，过P作直线PM⊥y轴于点M，过点A作直线AN⊥x轴于点N，交直线PM于点D，
若四边形OADP的面积为6．求P点的坐标．

已知反比例函数y=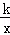的图象经过点P（1，6）．
（1）求k的值；
（2）若点M（﹣2，m），N（﹣1，n）都在该反比例函数的图象上，试比较m，n的大小．

如图，在平面直角坐标系xOy中，矩形OEFG的顶点E坐标为（4，0），顶点G坐标为（0，2）．将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．

（1）判断△OGA和△NPO是否相似，并说明理由；
（2）求过点A的反比例函数解析式；
（3）若（2）中求出的反比例函数的图象与EF交于B点，请探索：直线AB与OM是否垂直，并说明理由．

如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数的图象的两个交点．

（1） 求此反比例函数的解析式及n的值；
（2） 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

如图，▱ABCD放置在平面直角坐标系中，已知点A（2，0），B（6，0），D（0，3），反比例函数的图象经过点C．

（1）求反比例函数的解析式；
（2）将▱ABCD向上平移，使点B恰好落在双曲线上，此时A，B，C，D的对应点分别为A′，B′，C′，D′，且C′D′与双曲线交于点E，求线段AA′的长及点E的坐标．

如图，在平面直角坐标系中，O为原点，直线AB分别与x轴、y轴交于B和A，与反比例函数的图象交于C、D，CE⊥x轴于点E，tan∠ABO=，OB=4，OE=2．

（1）求直线AB和反比例函数的解析式；
（2）求△OCD的面积．

如图，在直角坐标系xOy中，一直线y=2x+b经过点A（-1，0）与y轴正半轴交于B点，在x轴正半轴上有一点D，且OB=OD，过D点作DC⊥x轴交直线y=2x+b于C点，反比例函数y=（x＞O）经过点C．

（1）求b，k的值；
（2）求△BDC的面积；
（3）在反比例函数y=（x＞0）的图象上找一点P（异于点C），使△BDP与△BDC的面积相等，求出P点坐标．