初中数学坐标与图形变化-旋转填空题

已知点A（1，5），B（3，1），点M在x轴上，当AM﹣BM最大时，点M的坐标为      ．

坐标平面上，在第二象限内有一点P，且P点到x轴的距离是7，到y轴的距离是9，则P点坐标为          ．

在平面直角坐标系中，A（-4，0），B（-4，4），C、D在y轴上，点C在点D上方，CD=2．要使得四边形ABCD的周长最短，则点C的坐标为             ．

如图，平面直角坐标系中有一个正六边形ABCDEF，其中C．D的坐标分别为（1，0）和（2，0）．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A，B，C，D，E，F中，会过点（2015，2）的是点         ．

点C在x轴上方，y轴右侧，距离x轴4个单位长度，距离y轴3个单位长度，则点C的坐标为           ．

在平面直角坐标系xOy中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A₁的伴随点为A₂，点A₂的伴随点为A₃，点A₃的伴随点为A₄，…，这样依次得到点A₁，A₂，A₃，…，A_n，…．若点A₁的坐标为（3，1），则点A₃的坐标为                ，点A₂₀₁₄的坐标为              ；若点A₁的坐标为（a，b），对于任意的正整数n，点A_n均在x轴上方，则a，b应满足的条件为                            ．

已知点A（a，0）和点B（0，5）两点，且直线AB与坐标轴围成的三角形的面积等于10，则a的值是              ．

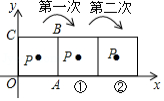
如图，把正方形铁片 $\mathit{OABC}$置于平面直角坐标系中，顶点 $A$的坐标为 $(3,0)$，点 $P(1,2)$在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转 $90°$，第一次旋转至图①位置，第二次旋转至图②位置 $\dots$，则正方形铁片连续旋转2017次后，点 $P$的坐标为　　．

如图，平面直角坐标系中，矩形 $\mathit{OABC}$的顶点 $A(-6,0)$， $C(0$， $2\sqrt{3})$．将矩形 $\mathit{OABC}$绕点 $O$顺时针方向旋转，使点 $A$恰好落在 $\mathit{OB}$上的点 $A_1$处，则点 $B$的对应点 $B_1$的坐标为　　．

如图，已知点 $A(2,0)$， $B(0,4)$， $C(2,4)$， $D(6,6)$，连接 $\mathit{AB}$， $\mathit{CD}$，将线段 $\mathit{AB}$绕着某一点旋转一定角度，使其与线段 $\mathit{CD}$重合（点 $A$与点 $C$重合，点 $B$与点 $D$重合），则这个旋转中心的坐标为　 　．

如果甲图形上的点P（-2,4）经平移变换后是Q（3,2）,则甲图上的点M（1,-2）经这样平移后的对应点的坐标是           ．

如图，在平面直角坐标系中，四边形OABC是边长为2的正方形，顶点A、C分别在x，y轴的正半轴上．点Q在对角线OB上，且QO=OC，连接CQ并延长CQ交边AB于点P．则点P的坐标为     ．

如图，在直角坐标系中，点A、B、C的坐标分别为（0，3）（4，3）（0，－1），则△ABC外接圆的圆心坐标为      ．

若点A（4，1－2m）在x轴上，则m＝            ．

如果点P（4，）和点Q（a，b）关于y轴对称，则a=         ，b=        ．