(本题8分)在平面直角坐标系xOy中,已知点P(3,4),点Q在x轴上,△PQO是等腰三角形,在图中标出满足条件的点Q位置,并写出其坐标.
在直角坐标系中,将坐标(0,0)、(0,4)、(2,0)、 (4,4)的点用线段依次连接起来,形成一个图形.
(1)在直角坐标系中画出该图形,并说明该图形是什么形状?
(2)若每个点的纵坐标不变,横坐标分别乘以-1,则所得图形与原图形有什么关系?
已知在正方形的网格中,网线的交点称为格点,如图,点A、B、C都是格点.每个小正方形的边长为1个单位长度,若在网格中建立坐标系,则A的坐标为(-1,3),B的坐标为(1,3),C的坐标为(3,1).
(1)利用正方形网格,直接用圆规作过A、B、C三点的圆,并写出圆心O的坐标;
(2)在(1)中所作的⊙O外,在这8×8的网格中找到一个格点P,作△PAC,使得△PAC的面积与△ABC的面积相等,并写出点P的坐标.(写出一个即可)
如图,一只甲虫在.的方格(每小格边长为1)上沿着网格线运动。它从A处出发去看望B、C、D处的其他甲虫。规定:向上、向右走为正,向下、向左走为负。如从A到B记为: (+1,+4),从B到A记为:
(+1,+4),从B到A记为: (-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中
(-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)填空: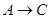 ( , 4 ),
( , 4 ), ( , ),
( , ), ( +1 ,—2 ),
( +1 ,—2 ), (2)若这只甲虫的行走路线为
(2)若这只甲虫的行走路线为 ,请计算该甲虫走过的路程;
,请计算该甲虫走过的路程;
(3)若这只甲虫从A处去甲虫P处的行走路线一次为(+1,+2),(+2,—1),(—2,+3),(—1,—2),请在图中标出P的位置。
如图,某校7年级的学生从学校O点出发,要到某地P处进行探险活动,他们先向正西方向走8km到A处,又往正南方向走4km到B处,又折向正东方向走6km到C处,再折向正北方向走8km到D处,最后又往正东方向走4km才到探险地P;取点O为原点,取点O的正东方向为x轴的正方向,取点O的正北方向为y轴的正方向,以2km为一个单位长度建立平面直角坐标系.
(1)在平面直角坐标系中画出探险路线图;
(2)分别写出A、B、C、D、P点的坐标.
如图, 在平面直角坐标系 中, 点
中, 点 (0,8), 点
(0,8), 点 (6 , 8 ).
(6 , 8 ).
(1)只用直尺(没有刻度)和圆规, 求作一个点 ,使点
,使点 同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
同时满足下列两个条件:(要求保留作图痕迹, 不必写出作法):
①点P到 、
、 两点的距离相等;②点P到
两点的距离相等;②点P到 的两边的距离相等.
的两边的距离相等.
(2) 在(1)作出点 后, 在图上写出点
后, 在图上写出点 的坐标.
的坐标.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标我(4,-1).
(1)把△ABC向上平移5个单位后得到对应的△ ,画出△
,画出△ 的图形并写出点
的图形并写出点 的坐标;
的坐标;
(2)以原点O为对称中心,再画出与△ 关于原点对称的△
关于原点对称的△ ,并写出点
,并写出点 的坐标.
的坐标.
如图,已知点A的坐标分别为(3,4),将线段OA沿x轴向左平移5个长度单位,得到线段CB(点C在x轴上).
(1)请分别写出点B、C的坐标:B ,C ;
(2)画出线段CB,并连结AB;
(3)试问四边形ABCO的形状如何?请说明理由,并求出其面积.
在平面直角坐标系中,四边形ABCD的各个顶点的坐标分别是
A(0,0),B(2,5),C(9,8),D(12,0)
⑴请画出平面直角坐标系,并在直角坐标系中画出四边形ABCD。
⑵求出四边形ABCD的面积。
如图是某学校的平面示意图,在8×8的正方形网格中,如果实验楼所在位置的坐标为(-2,-3).
(1)请画出符合题意的平面直角坐标系;
(2)在(1)的平面直角坐标系内表示下列位置:旗杆 ;校门 ;图书馆 ;教学楼 .
如图是建有平面直角坐标系的正方形网格,请按下列要求操作:
(1)画 ,使
,使 三点的坐标分别为
三点的坐标分别为 ;
;
(2) 种特殊的四边形?
种特殊的四边形?
请在所给网格中按下列要求操作:
⑴ 请在网格中建立平面直角坐标系,使 点坐标为(0,2),
点坐标为(0,2), 点坐标为(-2,0);
点坐标为(-2,0);
⑵ 在(1)的条件下,在平面坐标系中确定点C,使△ 为等腰直角三角形,请画出所有符合条件的点
为等腰直角三角形,请画出所有符合条件的点 ,并直接写出相应的
,并直接写出相应的 点坐标.
点坐标.
在平面直角坐标系中(如图每格一个单位),⑴画出下列各点(-2,-1),(2,-1),(2,2),(3,2)(0,3),(-3,2),(-2,2), (-2,-1)并依次将各点连结起来(说说所连图形象什么),⑵所得图形整体向右平移2个单位,说出对应点的坐标发生了怎样的变化? 
在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
(1)在下列坐标系中画出这个图案;
(2)若将上述各点的横坐标保持不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连接起来,所得的图案与原图案相比有什么变化?