[山东]2011—2012学年山东潍坊八年级下期末模拟数学试卷
如图:AB∥DE,CD=BF,若△ABC≌△EDF,还需补充的条件可以是
| A.∠B=∠E | B.AC="EF" | C.AB=ED | D.不用补充条件 |
如图,身高1.6m的学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0m,BC=8.0m,则旗杆的高度是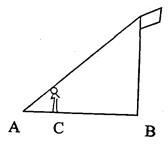
| A.6.4m | B.7.0m | C.8.0m | D.9.0m |
如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是
| A.AB=CD | B.AD=BC | C.AB=BC | D.AC=BD |
汶川地震后,某电视台法制频道在端午节组织发起“绿丝带行动”,号召市民为四川受灾的人们祈福.人们将绿丝带剪成小段,并用别针将折叠好的绿丝带别在胸前,如图所示,绿丝带重叠部分形成的图形是
| A.正方形 | B.等腰梯形 | C.菱形 | D.矩形 |

如图,将矩形ABCD沿DE折叠,使A点落在BC边上F处,若∠EFB=70°,则∠AED= 
| A.80° | B.75° | C.70° | D.65° |
如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的
| A.三角形 | B.平行四边形 | C.矩形 | D.正方形 |

已知点( ,
, ),(
),( ,2),(
,2),( ,3)都在反比例函数
,3)都在反比例函数 的图象上,则下列关系中正确的是
的图象上,则下列关系中正确的是
A. |
B. |
C. |
D. |
有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况如图所示:根据条形图提供的信息,下列说法中,正确的是
| A.两次测试,最低分在第二次测试中 |
| B.第一次测试和第二次测试的平均分相同 |
| C.第一次分数的中位数在20~39分数段 |
| D.第二次分数的中位数在60~79分数段 |
农机厂职工到距工厂15千米的某地检修农机,一部分人骑自行车先走半小时后,其余人乘汽车出发,结果他们同时到达,已知汽车速度为自行车速度的3倍,若设自行车的速度为x千米/时,则所列方程为
A. |
B. |
C. |
D. |
湖北省发改委办公室2008年1月24日公布:2007年,武汉市宏观经济运行态势良好,城市居民生活水平明显提高,居民人均可支配收入水平和人均消费性支出均呈两位数增长.2007年,武汉市城市居民人均可支配收入为14358元,比上年同期实际增长11.6%.如图是居民人均可支配收入每年比上年增长率的统计图(如图①)和人均消费性支出的统计图(如图②).
根据图中信息,下列说法:①在这五年中我市居民人均可支配收入最多的是2006年;②2007年我市居民人均消费性支出占人均可支配收入的比例约为73.8%;③2006年我市居民人均消费性支出占人均可支配收入的比例为 .其中正确的有
.其中正确的有
| A.①②③ | B.只有①② | C.只有②③ | D.只有② |
已知:如图,在正方形ABCD中,P为对角线AC上的一动点,PE⊥AB于E,PF⊥BC于F,过点P作DP的垂线交BC于点G,DG交AC于点Q.下列说法:①EF=DP;②EF⊥DP;③ ;
;
④ .其中正确的是
.其中正确的是
| A.①②③④ | B.①②③ | C.①②④ | D.①③④ |

如图,观察图中菱形的个数:图1中有1个菱形,图2中有5个菱形,图3中有14个菱形,图4中有30个菱形……,则第6个图中菱形的个数是 个.
如图,已知A(0,-3),B(2,0),将线段AB平移至DC的位置,其D点在x轴的负半轴上,C点在反比例函数 的图象上,若S△BCD=9,则k=___________.
的图象上,若S△BCD=9,则k=___________.
2008年5月12日,四川省汶川县发生8.0级大地震. 某校学生会倡导“抗震救灾,众志成城”自愿捐款活动并进行了抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为2:4:5:8:6.又知此次调查中捐款20元和25元的学生一共28人.
⑴他们一共调查了多少人?
⑵这组数据的众数、中位数是多少?
⑶若该校共有2000名学生,估计全校学生大约捐款多少元?
如图,已知点A的坐标分别为(3,4),将线段OA沿x轴向左平移5个长度单位,得到线段CB(点C在x轴上).
(1)请分别写出点B、C的坐标:B ,C ;
(2)画出线段CB,并连结AB;
(3)试问四边形ABCO的形状如何?请说明理由,并求出其面积.
如图,ABCD为平行四边形,AD=2,BE∥AC,DE交AC的延长线于F点,交BE于E点.
(1)求证:EF=DF;
(2)若AC=2CF,∠ADC=60 o, AC⊥DC,求DE的长.
一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用6小时到达目的地.
(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)如果该司机匀速返回时,用了4.8小时,求返回时的速度;
(3)若返回时,司机全程走高速公路,且匀速行驶,根据规定:最高车速不得超过每小时120公里,最低车速不得低于每小时60公里,试问返程时间的范围是多少?
已知:如图,梯形ABCD中,AD∥BC,∠ABC=90°.
(1)如图1,若AC⊥BD,且AC=5,BD=3,则S梯形ABCD= ;
(2)如图2,若DE⊥BC于E,BD=BC,F是CD的中点,试问:∠BAF与∠BCD的大小关系如何?请写出你的结论并加以证明;
(3)在(2)的条件下,若AD=EC, = .
= .
 与x轴、y轴所围成的三角形的面积为
与x轴、y轴所围成的三角形的面积为

 与反比例函数
与反比例函数 的图象交于点
的图象交于点 ,则使
,则使 的
的 的取值范围是 .
的取值范围是 . 

 ,其中
,其中

 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号